Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 1
Dado o gráfico de uma função :
- Obtenha o valor de .
- Estime o valor de .
- para quais valores de x?
- Estime os valores de x para os quais .
- Obtenha o domínio e imagem de .
- Em qual intervalo é crescente?
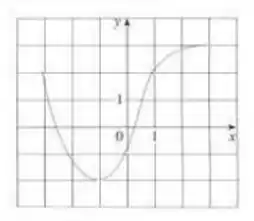
Passo 1
E aii galerinha do responde ai, bora resolver mais uma?
Vou dar umas dicas importantíssimas para resolver essa questão e as demais que são similares, então já anota ai!!
a) Para obtermos o valor de :
- No gráfico da função localize o ponto onde ;
- Olhe para o valor correspondente no eixo vertical (ordenada) desse ponto.
Esse será o valor de .
Logo o valor será igual à (, pois e notória que cada “quadradinho” , para este caso podemos afirmar que equivale à +/- 1.
Passo 2
b) Estime o valor de :
- Iremos procurar no gráfico o ponto onde .
- Faça uma estimativa do valor de , baseando-se na altura desse ponto no gráfico.
é próximo de 3, porém menor que 3.
Portanto, uma boa estimativa nesse caso é:
Passo 3
c) para quais valores de ?:
- Identifique no gráfico os pontos onde a altura da função é 2.
- Esses serão os valores de para os quais
Precisamos olhar na linha horizontal aonde que a curva da função bate, e olhar nesse pontos quais são os valores de x. São eles:
e
Passo 4
d) Estime os valores de x para os quais :
- Busque no gráfico onde a função cruza o eixo x, ou seja, onde a altura da função é zero.
- Estime os valores de correspondentes a esses pontos de cruzamento.
O gráfico de corta o eixo em dois pontos, e eles são e . Logo:
e
Passo 5
e) Obtenha o domínio e imagem de :
- O domínio de uma função é o conjunto de todos os valores de para os quais a função é definida. No gráfico, observe onde a função está traçada, isso indica o domínio.
- A imagem é o conjunto de todos os valores de que a função pode assumir. No gráfico, observe a faixa vertical coberta pela função para determinar a imagem.
Logo, Olhando para o gráfico, vemos que a função está definida para , portanto, o Domínio de é .
Ainda no gráfico, vemos que assume todos os valores entre . Logo, a Imagem de é .
Passo 6
f) Em qual intervalo f é crescente?
- Uma função é crescente em um intervalo se, ao percorrer da esquerda para a direita nesse intervalo, os valores da função aumentam.
- No gráfico, localize onde a função está ascendente ao longo do eixo x. Essa será a região onde a função é crescente.
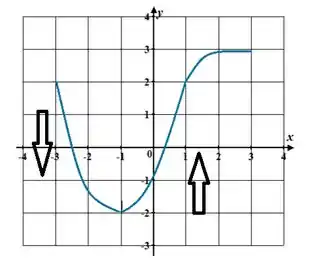
Uma função é dita crescente num intervalo quando para quaisquer e em .
Olhando para o bendito gráfico pela última vez, vemos que só é crescente no intervalo
Resposta
e
só é crescente no intervalo