Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 11
Descreva a região cuja área é dada pela integral
Passo 1
E aí meus queridxs, tudo bom com vocês? Se liguem só, vamos entender o que tá acontecendo aqui nessa questão e o que ela deseja da gente. Diferente das duas questões anteriores onde ele dava a região e pedia pra gente escrever a integral de forma iterada, para essa questão nós já temos a integral iterada e vamos precisar descrever a região. Pois bem, se observarmos bem a integral está na forma polar e poderemos escrevê-la da seguinte forma alternativa
Pela variação de sabemos que nossa região se encontra no primeiro quadrante e é uma representação da função . Dessa forma, plotando em algum software matemático vamos encontrar
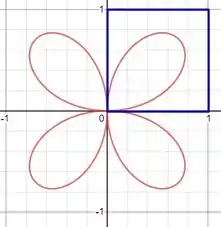
Pronto, tá resolvido nosso problema. Até que foi tranquilo, né?
Resposta
Exercícios de Livros Relacionados
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ D x yd A , onde D é o disco com centro na origem e raio 3 .
Calcule a integral dada, colocando-a em coordenadas polares. ∫ ∫ R cos x 2 + y 2d A , onde R é a região acima do eixo x e dentro da circunferência x 2 + y 2 = 9 .
Esboce a região cuja área é dada pela integral e calcule-a. ∫ π 2 π ∫ 4 7 rd rd θ
Esboce a região cuja área é dada pela integral e calcule-a. ∫ 0 π / 2 ∫ 0 4 cos θ rd rd θ