Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.1 - Ex. 7

O deslocamento (em pés) de uma certa partícula movendo-se em linha reta é dado por s = t 3 6 .

  1. Encontre a velocidade média durante os períodos de tempo a seguir:

    2. i 1,3

    i i 1,2

    i i i 1 ,   1,5

    i v 1 ,   1,1

  2. Encontre a velocidade instantânea quando t = 1 .
  3. Faça um gráfico de s como uma função de t e trace retas secantes com inclinações iguais às velocidades médias encontradas na parte ( a ) .
  4. Trace a reta tangente cuja inclinação é a velocidade instantânea da parte ( b ) .

Passo 1

Olá, meu parceiro. Vamos dar início a mais uma resolução.

Aqui a gente tem a equação do deslocamento de uma partícula em relação ao tempo, e devemos encontrar a velocidade média dela em alguns intervalos de tempo, além da sua velocidade instantânea em t = 1 .

Deveremos também fazer os gráficos de s em função de t , mostrar no gráfico a inclinação das retas iguais as velocidades médias que encontrarmos no tópico a).

A velocidade média, que é o nosso primeiro desafio aqui, é dada da seguinte forma:

Δ V = Δ s Δ t

Onde Δ s é o deslocamento da partícula em um intervalo de tempo Δ t .

Passo 2

Letra a)

Então temos a nossa função do espaço:

s = t 3 6

Para o primeiro intervalo: [ 1 , 3 ]

v m e d = 3 3 6 - 1 3 6 3 - 1

= 27 6 - 1 6 2

= 26 6 ∙ 1 2

= 13 6   f t / s e c

Para o segundo intervalo: [ 1,2 ]

v m e d = 2 3 6 - 1 3 6 2 - 1

= 8 6 - 1 6 1

= 7 6 ∙ 1 1

v = 7 6   f t / s e c

Para o terceiro intervalo: [ 1 ,   1.5 ]

v m e d = 1.5 3 6 - 1 3 6 1.5 - 1

= 27 48 - 8 48 1 / 2

= 19 48 ∙ 2 1

v = 19 24   f t / s e c

Para o segundo intervalo: [ 1 ,   1.1 ]

v m e d = 1.1 3 6 - 1 3 6 1.1 - 1

= 1331 6 000 - 1 000 6 000 1 / 10

= 331 6 000 ∙ 1 0 1

v = 331 6 00   f t / s e c

Passo 3

Letra b)

A velocidade instantânea em t = 1 será dada quando tomarmos o limite da velocidade média em t → 1 :

lim h → 0 ⁡ s t + h - s ( t ) h

Substituindo:

lim h → 0 ⁡ t + h 3 6 - t 3 6 h

Realizando o produto notável:

lim h → 0 ⁡ h 3 + 3 h 2 t + 3 h t 2 + t 3 6 - t 3 6 h

Simplificando:

lim h → 0 ⁡ h 3 + 3 h 2 t + 3 h t 2 6 h

Organizando a fração:

lim h → 0 ⁡ h 3 + 3 h 2 t + 3 h t 2 h 6

Simplificando o h :

lim h → 0 ⁡ h 2 + 3 h 1 t + 3 t 2 6

Calculando de fato o limite, temos então:

Para t = 1 :

v = 1 2   f t / s

Passo 4

Letra c)

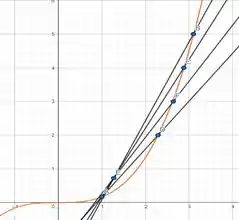
Na parte 7a, encontramos as velocidades médias da partícula para diferentes períodos de tempo.

Aqui está a função para o deslocamento da partícula medido em pés.

Observe que a velocidade média é a inclinação de cada uma das retas secantes.

m = v m e d

Os períodos de tempo serão os pontos que usaremos para a equação da reta secante.

Vamos começar com o intervalo:

1,3

y - y 1 = m x - x 1

y - 3 = 13 6 x - 1

y - 3 = 13 6 x - 13 6

y = 13 6 x + 5 6

Agora para o intervalo:

1,2

y - y 1 = m x - x 1

y - 2 = 7 6 x - 1

y - 2 = 7 6 x - 7 6

y = 7 6 x + 5 6

Agora para o intervalo:

1 , 1.5

y - y 1 = m x - x 1

y - 3 2 = 19 24 x - 1

y - 3 2 = 19 24 x - 19 24

y = 19 24 x + 17 24

Agora para o intervalo:

1,1 . 1

y - y 1 = m x - x 1

y - 11 10 = 331 600 x - 1

y - 11 10 = 331 600 x - 331 600

y - 660 600 = 331 600 x - 331 600

y = 331 600 x + 329 600

Aqui está a função com as retas secantes correspondentes, vamos gerar esse gráfico com o GeoGebra:

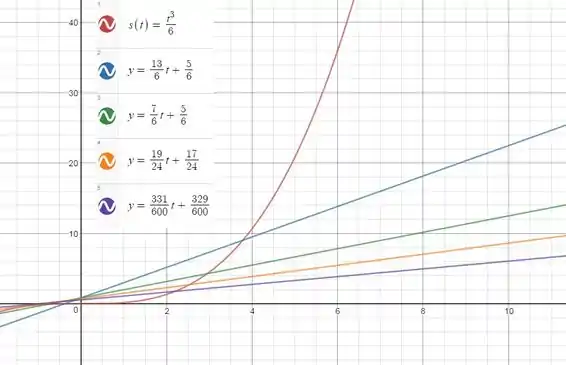
Passo 5

Letra d)

A reta tangente, que tem uma inclinação de 0.5, é fornecida na forma:

y = 0.5 x + n

e do fato de que o ponto 1 , s t = 1 , 1 6 pertence a ela, temos que:

1 6 = 1 2 + n

- 1 3 = n

Portanto, a reta tangente com a inclinação de 1 2 é dada pela equação:

y = 1 2 x - 1 3

Gerando o gráfico utilizando o GeoGebra:

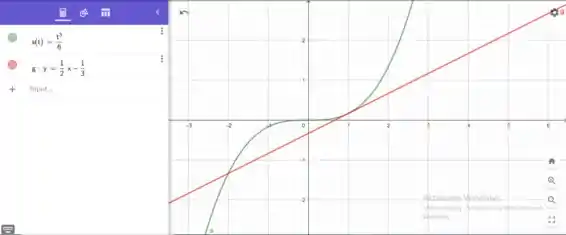
Resposta

( a )

i 1,3   e   h = 2 → v m = 13 6   f t / s

i i   1,2   e   h = 1 → v m = 7 6   f t / s

i i i 1,1.5   e   h = 0,5 → v m = 19 24   f t / s

i v 1,1.1   e   h = 0.1 → v m = 331 600   f t / s  

( b ) v = 1 2   f t / s

( c )

( d )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A reta s para pelo ponto 3,0 e é normal ao gráfico de f x = x 2 no ponto a , b .a) Determine a , b .b) Determine a equação de s .
Determine a equação de uma reta, não vertical, que passa pelo ponto 0 , 4 3 e que seja normal ao gráfico de y = x 3 .
Sejam A e B os pontos em que o o gráfico de f x = x 2 - α x , α real, intercepta o eixo x . Determine α para que as retas tangentes ao gráfico de f em A e em B , sejam perpendiculares.
Sabe-se que r é uma reta perpendicular à reta 3 x + y = 3 e tangente ao gráfico de f x = x 3 .Determine r .
Seja y = f x definida e derivável num intervalo contendo 1 e suponha que f seja dada implicitamente pela equação y 3 + x 2 y = 130 . Determine as equações das retas tangente e normal ao gráfico de f ,