Uma determinada empresa está interessada em maximizar o lucro mensal proveniente de dois de seus produtos, designados I e II. Para fabricar estes produtos ela utiliza um tipo de máquina que tem uma disponibilidade de 200 máquinas-hora por mês e um tipo de mão de obra com uma disponibilidade de 240 homens-hora por mês . Para se produzir uma quantidade do produto I utilizam-se 5 horas maquina e 10 horas mão de obra, quanto para o produto II, utilizam-se 4 horas maquina e 4 horas mao de obra. Espera-se uma demanda de 20 unidades por mês do produto I e 45 do II. Calcula-se o lucro por unidade de 10,00 para o produto I e 6,00 para o produto II. Determine as quantidades de cada produto que deverão ser fabricados pra o lucro ser máximo.

Sendo o produto I e o produto II temos que a função lucro é dada por .

A qual não possui pontos críticos e está determinada em

Vamos analisar os pontos de fronteira

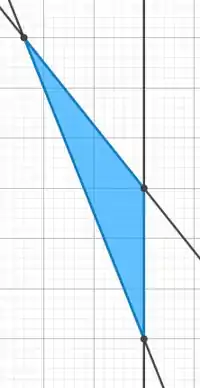
Temos os pontos . Aplicando a função,

,

Já

E

Logo, é maximo