Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 6b
Determinar, algebricamente, os intervalos nos quais as funções seguintes são crescentes ou decrescentes. Fazer um esboço do gráfico, comparando os resultados.
b)
Passo 1
Então pessoal, caso não se lembrem, por definição uma função é crescente se ela for contínua em um intervalo , derivável nesse mesmo intervalo e, por fim, se apresenta .
Por definição uma função é decrescente se ela for contínua em um intervlao , derivável nesse mesmo intervalo e ,por fim, se apresenta . Essas são as definições para intervalos crescentes e decrescentes de uma função e basta apenas isso e um pouco de intuição para resolvermos o problema, tudo jóia? Então bora lá!
Passo 2
Se derivarmos a função que nos foi dada, teremos:
Vocês devem concordar comigo que não existem valores de nos quais a função é positiva, logo, temos que:
Então é uma função decrescente para TODO valor de , o que faz sentido, uma vez que nossa é uma reta! Se esboçarmos o gráfico, teremos:
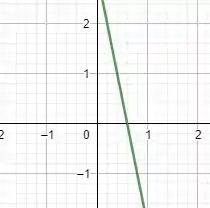
Portanto, a função é decrescente em
Resposta
Intervalos crescentes: Não existem.
Intervalos decrescentes:
