Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.4 - Ex. 62
Determine a área da região sombreada.
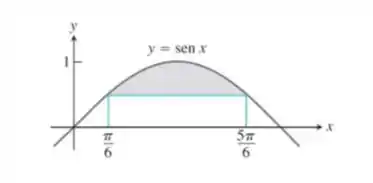
Passo 1
Para determinar a área da região sombreada de precisamos primeiramente definir o intervalo da função . Pela imagem é fácil perceber que ela é delimitada por e .
Logo, temos o seguinte intervalo .
Passo 2
Agora devemos integrar e substituir os limites de integração. Relembrando que de forma genérica ele é feito da seguinte maneira:
Ou seja, após integrar de forma genérica você irá substituir os limites de integração ( a e b) nesse resultado obtido, respeitando a ordem de o limite superior aplicado na função menos o limite inferior aplicado na função.
Assim:
Passo 3
Por fim, a área total é obtida pela adição dos valores absolutos da integral calculada. Logo:
Resposta
Exercícios de Livros Relacionados
Suponha que f tenha uma derivada positiva para todos os valores de x e que f 1 = 0 . Qual das seguintes afirmações deve ser verdadeira sobre a função g x = ∫ 0 x f td t Justifique sua resposta. g é um
Suponha que f ( 4 ) se ∫ 0 x f ( t )d t = x cos π x .
Determine a linearização deg (x) = 3 + int_1^(x^2) sec (t - 1) d t Em x = - 1 .
Suponha que int_1^x f ( t ) d t = x^2 - 2 x + 1 . Determine f ( x ) .
Determine lim x → ∞ 1 x∫ 1 x d t t