Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 60
Determine as áreas totais das regiões sombreadas
Passo 1
Precisamos determinar a área dada em cinza na figura da questão. Desta forma, se ao longo de um intervalo , então a área entre as curvas e é dada por:
Desta forma, temos que identificar em cada caso quem é , e o intervalo .
Passo 2
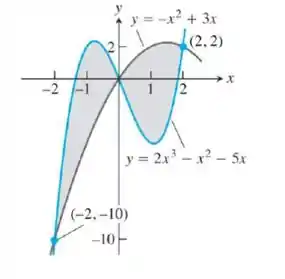
Vamos começar por montar qual a integral que devemos calcular. A área que devemos calcular é entre a função e . Além disto, observe a mudança do comportamento das funções. Entre , e entre o intervalo ocorre o contrário. Desta forma, a área da região em cinza é dada por:
Observe que é necessário separar em uma soma de integrais devido à mudança no comportamento da imagem das funções.
Passo 3
Estamos quase prontos para resolver a integral e a nossa questão. Só temos um leve problema. Afinal, quem é esse que aparece nos limites de integração? Ele é a coordenada do ponto de interseção entre as duas curvas. Antes dele nós tínhamos e depois dele . Portanto, basta igualar as duas funções e resolver a equação. Desta forma, temos:
Resolvendo a equação acima, obtemos , e . Como o ponto encontra-se “próximo” a origem do sistema de coordenadas, temos que . Portanto, a área é dada por:
Passo 4
Vamos resolver agora nossa integral.