Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 58
Determine as áreas totais das regiões sombreadas
Passo 1
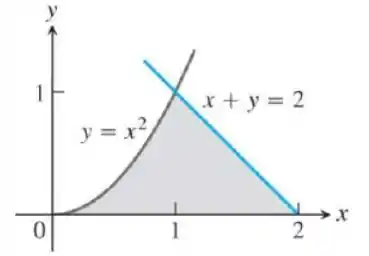
Precisamos determinar a área dada em cinza na figura da questão. Observe que a região é limitada a esquerda por uma curva e a direita por outra curva , além disto, é limitada inferiormente por e superiormente por . Desta forma, podemos expressar a área desta região a partir da seguinte integral:
Desta forma, temos que identificar em cada caso quem é , e o intervalo .
Passo 2
Vamos começar por montar qual a integral que devemos calcular. A curva , que limita o nosso intervalo a direita, é obtido através da seguinte equação: . Se isolarmos o , obteremos . Já a função , que limita a nossa região a esquerda, é dada por .
Temos que determinar agora o nosso intervalo de integração. A região é limitada inferiormente pela reta . Já o limite superior é dado pela interseção das duas curvas. Desta forma, vamos resolver a seguinte equação:
Portanto, as únicas soluções são e . Como pode ser confirmado através da escala, a nossa região é limitada superiormente por . Desta forma, a área em cinza pode ser expressa através da seguinte integral:
Passo 3
Vamos resolver agora a nossa integral.