Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.2 - Ex. 1p
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários).
Passo 1
Oi, pessoal! Tudo bom? Nessa questão primeiro vamos ter que achar e depois analisar seu sinal.
Para isso vamos usar a regra do produto:
Lembrando que,
Vamos então aplicar:
Ajeitando,
Passo 2
Agora vamos analisar o sinal de , igualando a zero:
Assim:
Temos que em:
Ou seja, é estritamente crescente em
E em :
OU seja, é estritamente decrescente em
Passo 3
Para esboçar o gráfico vamos calcular os limites de para e :
Pronto, agora podemos esboçar o gráfico, ficando desse jeito:
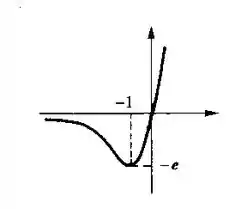
Resposta
é estritamente crescente em
é estritamente decrescente em
Exercícios de Livros Relacionados
Seja f x = x 2 sin 1 x .(a)Os limites lim x → 0 + f ( x ) e lim x → 0 - f ( x ) são formas indeterminadas?(b)Use um recurso computacional para gerar o gráfico de f e use o gráfico para fazer con
Se x 1x 2 , que relação deve existir entre f ( x 1 ) e f ( x 2 ) para f ser crescente em um intervalo contendo x 1 e x 2 ? Decrescente? Constante ?Qual condição f ' garante que f seja crescente em um
Qual condição sobre f ' garante que, em um intervalo aberto, f seja: côncava para cima, côncava para baixo?Qual condição sobre f ' ' garante que, em um intervalo aberto, f seja: côncava para cima, côn
Use o gráfico da equação y = f ' ' ( x ) na figura Ex-5 para determinar as coordenadas x de todos os pontos de inflexão de f . Explique seu raciocínio.
Suponha que f seja diferenciável em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.11.Se f for decrescente em [ 0 ,2 ] , então f 0f 1f ( 2 ) .