Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.5 - Ex. 7

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ .

D é delimitada por y = e x   ,   y = 0   ,   x = 0   e x = 1 ; ρ x ,   y = y

Passo 1

Galera, tudo certo?

Esse exercício pede pra acharmos o valor da massa e do centro de massa de uma lâmina, dada a região D que ela ocupa e sua função densidade ρ x ,   y = y .

Com essas informações, conseguimos calcular a massa com essa integral:

m = ∬ D ρ ( x ,   y ) d A

A coordenada x do centro de massa calculamos assim:

x - = 1 m ∬ D x   ρ x , y d A

E a coordenada y :

y - = 1 m ∬ D y   ρ x , y d A

Nosso primeiro passo vai ser definir os limites de integração das variáveis a partir da região D , então conseguimos transformar essas integrais em integrais iteradas.

Daí, vamos calcular as integrais, de dentro pra fora.

Passo 2

Bom, vamos esboçar essa região D , que é limitada por:

y = e x   ,   y = 0

x = 0 ,   x = 1

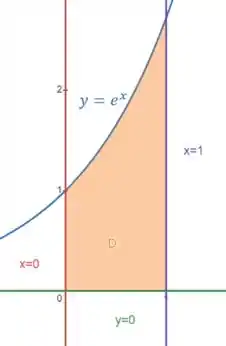
Como nossa região está abaixo de e x e acima de y = 0 , temos:

0 ≤ y ≤ e x

E com relação a x , está entre 0 e 1 :

0 ≤ x ≤ 1

Percebe que quando formos aplicar isso nas integrais, o y tem que ficar mais pra dentro, porque seus limites dependem de x .

Com isso, já conseguimos calcular nossas integrais.

Passo 3

Primeiro vamos calcular a massa:

m = ∬ D ρ x ,   y d A = ∫ 0 1 ∫ 0 e x y d y d x

Calculando em função de y , com x constante:

∫ 0 1 ∫ 0 e x y d y d x =

= ∫ 0 1 y 2 2 0 e x d x =

Substituindo nos limites de integração:

= ∫ 0 1 e 2 x 2 - 0 d x =

Agora integramos em função de x :

= ∫ 0 1 e 2 x 2 d x =

A primitiva de e 2 x é e 2 x 2 , então:

= e 2 x 4 0 1

= e 2 4 - e 0 4

Então:

m = e 2 - 1 4

Passo 4

Agora vamos calcular x - , pra saber qual é o centro de massa x - ,   y - :

x - = 1 m ∬ D x   ρ x ,   y d A = 4 e 2 - 1 ∫ 0 1 ∫ 0 e x x y d y d x

Calculando em função de y , com x constante:

4 e 2 - 1 ∫ 0 1 ∫ 0 e x x y d y d x =

= 4 e 2 - 1 ∫ 0 1 x y 2 2 0 e x d x =

Aplicando os limites:

= 4 e 2 - 1 ∫ 0 1 x e 2 x 2 - 0 d x =

Colocando o 1 2 em evidência, vamos integrar em função de x :

= 4 e 2 - 1 ∙ 1 2   ∫ 0 1 x ∙ e 2 x d x =

= 2 e 2 - 1   ∫ 0 1 x ∙ e 2 x d x =

Vamos usar integração por partes:

u = x ⇒ d u = d x

d v = e 2 x d x ⇒ v = e 2 x 2

Então

= 2 e 2 - 1 ∙ x ∙ e 2 x 2 - ∫ e 2 x 2 d x 0 1 =

= 2 e 2 - 1 ∙ x ∙ e 2 x 2 - e 2 x 4 0 1 =

Substituindo os limites de integração:

= 2 e 2 - 1 ∙ 1 ∙ e 2 2 - e 2 4 - 0 - e 0 4 =

= 2 e 2 - 1 ∙ e 2 2 - e 2 4 + 1 4 =

Juntando as frações:

= 2 e 2 - 1 ∙ 2 e 2 - e 2 + 1 4 =

x - = e 2 + 1 2 e 2 - 1

Passo 5

Show! Agora só falta calcular y - :

y - = 1 m ∬ D y   ρ x ,   y d A = 4 e 2 - 1 ∫ 0 1 ∫ 0 e x y 2 d y d x

Primeiro integrando em função de y , com x constante:

4 e 2 - 1 ∫ 0 1 ∫ 0 e x y 2 d y d x =

= 4 e 2 - 1 ∫ 0 1 y 3 3 0 e x d x =

Resolvendo nos limites:

= 4 e 2 - 1 ∫ 0 1 e 3 x 3 - 0 d x =

= 4 e 2 - 1 ∫ 0 1 e 3 x 3 d x =

Agora integramos em função de x . Como a primitiva de e 3 x é e 3 x 3 ,

= 4 e 2 - 1 e 3 x 9 0 1 =

= 4 e 2 - 1 e 3 9 - e 0 9 =

Calculando:

= 4 e 2 - 1 ∙ e 3 - 1 9 =

⇒ y - = 4 e 3 - 1 9 e 2 - 1

E então:

x ,   - y - = e 2 + 1 2 ( e 2 - 1 ) , 4 ( e 3 - 1 ) 9 e 2 - 1

Resposta

m = e 2 - 1 4

x ,   - y - = e 2 + 1 2 ( e 2 - 1 ) , 4 ( e 3 - 1 ) 9 e 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a massa e o centro de massa da lâmina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap o ry = x + 2e y = x 2 ; ρ x , y = k x 2 é
Encontre a massa e o centro de massa da lâmina que ocupa a região D e é dada pela função da densidade ρ . Dél i m i t a d ap e l a sc u r v a sy = e - x ,y = 0 ,x = 0 ,x = 1 ; ρ x , y = x y é
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D está limitada pelo laço direito
Uma lamina tem a forma da região plana R delimitada pelas curvas x=y 2ex = 4 . Sua densidade de massa é constante. Determinar:a) O momento de inercia da lamina em relação ao eixo xb) O momento de iner
Uma lamina tem a forma do triangulo de vértices (-1,0), (1,1) e (1,-1). Determinar a massa e o centro de massa da lâmina se:a) Sua densidade de massa é constanteb) Sua densidade no ponto P(x,y) é prop