Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.6 - Ex. 24
Determine se a série é absolutamente convergente, condicionalmente convergente ou divergente.
24-
Passo 1
Quando se olha para a função arco tangente dá até um frio na espinha não é verdade? Mas relaxa que há uma esperança de deixar isso mais simples!
Reparou que tanto o numerador quanto o denominador estão elevados a ? Então... isso nos diz que podemos fazer o teste da raiz:
Onde será:
Não se esqueça de aplicar o módulo em .
Passo 2
Fazendo o teste da raiz nós teremos:
Porém se formos ver o gráfico da arco tangente conseguimos ver que:
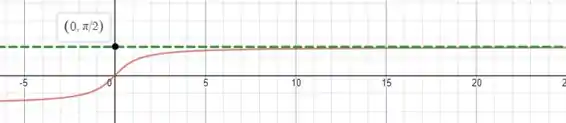
Que a medida que vai para infinito, a função arco tangente se aproxima cada vez mais de .
Outra forma de se ver isso é que normalmente dizemos que:
Logo aplicando o limite temos:
Já que logo :
O que nos dá pelo teste da raiz uma série absolutamente convergente.
Resposta
Série absolutamente convergente.