Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 11.Exercícios - Ex. 297
Resolva o sistema
Passo 1
Oi, pessoal! Tudo joia?
Para resolver esse sistema precisamos achar os valores de x e y para essas condições apresentadas nas equações. Temos duas equações e duas incógnitas, ou seja, conseguimos obter a resposta.
Primeiro vamos analisar qual relação se dá entre x e y na 1ª equação, logo após juntaremos essa relação com a 2ª equação e iremos realizar uma operação levando em conta elas duas. Por fim, chegaremos nos valores das nossas incógnitas.
Vamos lá!
Passo 2
Observando o ciclo trigonométrico abaixo conseguimos ver a relação dos valores das funções trigonométricas seno e cosseno com o ângulo para um .
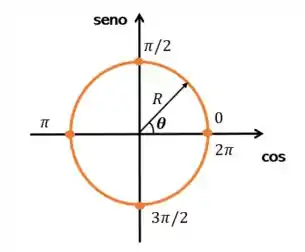
Para o seno de um ângulo qualquer ser igual a zero significa que esse ângulo pode assumir os valores de ou de zero e seus respectivos múltiplos.
Matematicamente falando, isso significa que:
Onde é um número inteiro.
Isto é, alguns valores de ângulos para o seno ser zero são:
Passo 3
Ok! Agora vamos pegar essa relação e juntar com a 2ª equação.
Somando essas duas equações teremos o cancelamento das incógnitas , pois eles têm sinais diferentes e restará apenas o . O resultado será:
Beleza, achamos o valor de , agora vamos substituir esse valor em uma das equações e achar quem é o .
Passo 4
Substituindo o valor de na 2ª equação, temos:
Prontinho galera, encontramos o . Fim da questão!