Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 23

Determine o volume do sólido que é limitado pelo cone z = x 2 + y 2 e pela esfera x 2 + y 2 + z 2 = 2

Passo 1

Faaala, pessoal!

Nessa questão a gente precisa achar o volume de um sólido limitado entre duas superfícies.

Vamos chamar esse sólido de W . O volume dele é calculado assim:

V W = ∭ W d V

Só que pra calcular essa integral, vamos ter que usar coordenadas cilíndricas – a gente vai ver com mais calma, mas isso acontece porque o sólido tem simetria com o eixo z . Então vamos relembrar a relação entre os sistemas de coordenadas cartesiano e cilíndrico:

x = r cos ⁡ θ y = r sen ⁡ θ z = z

Lembrando que r é sempre positivo, e o jacobiano dessa mudança é J = r .

Então vamos fazer essa mudança de variáveis, transformar nossa integral em uma integral iterada e calcular (de dentro pra fora).

Passo 2

Vamos começar olhando pras superfícies.

Uma delas é um cone z = x 2 + y 2 , como z ≥ 0 , só estamos falando da parte de cima do cone. E a outra é a esfera x 2 + y 2 + z 2 = 2 , centrada na origem e de raio 2 :

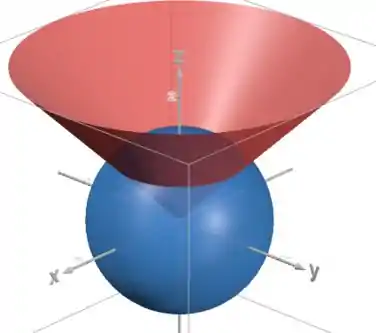
Assim, a gente consegue desenhar o sólido:

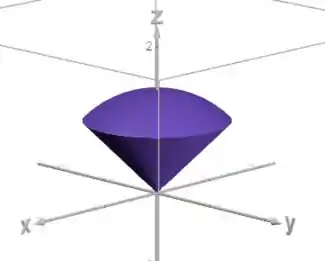
Ou seja, nosso sólido está abaixo da esfera e acima do cone.

Como está acima do cone, o valor de z é maior do que o valor de z do cone:

z ≥ x 2 + y 2

Como está abaixo da esfera, o valor de z é menor que o valor de z da esfera, então vamos isolar o z :

x 2 + y 2 + z 2 = 2

z 2 = 2 - x 2 - y 2

Só que estamos na região positiva de z , então

z = 2 - x 2 - y 2

Ou seja, para o nosso sólido:

z ≤ 2 - x 2 - y 2

Assim, achamos os limites de z :

x 2 + y 2 ≤ z ≤ 2 - x 2 - y 2

Passo 3

Voltando pro esboço do sólido:

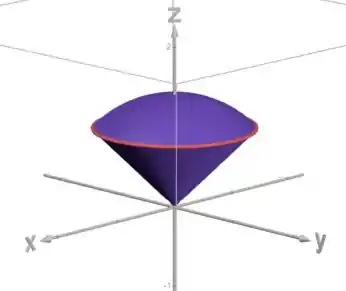
Percebe que o sólido é simétrico em volta do eixo z , ele é um sólido de. Então vamos usar coordenadas cilíndricas. Outra forma de perceber isso é que a projeção do sólido no plano x y é um círculo (vamos ver essa projeção já já).

A relação entre coordenadas cartesianas e cilíndricas é:

x = r cos ⁡ θ y = r sen ⁡ θ z = z

Projetando o sólido no plano x y , temos um círculo limitado por essa circunferência vermelha que aparece no desenho. Essa circunferência é a interseção das duas superfícies:

z = x 2 + y 2 ⇒ z 2 = x 2 + y 2

z 2 = 2 - x 2 - y 2

Igualando z 2 das duas equações:

2 - x 2 - y 2 = x 2 + y 2

x 2 + y 2 = 1

Ou seja, ela projetada é a circunferência de raio 1 centrada na origem:

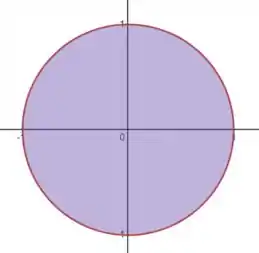
Para coordenadas cilíndricas, isso quer dizer que:

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Voltando para os limites de z :

x 2 + y 2 ≤ z ≤ 2 - x 2 - y 2

Como nesse sistema de coordenadas, temos

x 2 + y 2 = r 2

⇒ - x 2 - y 2 = - r 2

Então:

r 2 ≤ z ≤ 2 - r 2

r ≤ z ≤ 2 - r 2

Uma coisa importante: como os limites de z dependem de r , a gente tem que integrar em função de z primeiro! Então nossa integral fica assim:

V W = ∭ W d V = ∫ 0 1 ∫ 0 2 π ∫ r 2 - r 2 r d z d θ d r

Passo 4

Agora vamos integrar isso aí!

Sempre de dentro pra fora, então primeiro em função de z , considerando r e θ constantes:

∫ 0 1 ∫ 0 2 π ∫ r 2 - r 2 r d z d θ d r =

Como o r é constante, podemos tirar dessa primeira integral, e calculamos:

= ∫ 0 1 ∫ 0 2 π r ∙ ∫ r 2 - r 2 d z d θ d r =

= ∫ 0 1 ∫ 0 2 π r ∙ z r 2 - r 2 d θ d r =

Então, substituindo nos limites:

= ∫ 0 1 ∫ 0 2 π r ∙ 2 - r 2 - r d θ d r =

Agora vamos integrar em função de θ , com r constante. Então podemos tirar o integrando (que só depende de r ) dessa integral:

= ∫ 0 1 ∫ 0 2 π r ∙ 2 - r 2 - r d θ d r =

= ∫ 0 1 r ∙ 2 - r 2 - r ∙ ∫ 0 2 π d θ d r =

E resolvemos a integral:

= ∫ 0 1 r ∙ 2 - r 2 - r ∙ θ 0 2 π d r =

= ∫ 0 1 r ∙ 2 - r 2 - r ∙ 2 π - 0 d r

Passo 5

Por último, vamos integrar em função de r . Vamos tirar a constante 2 π - 0 = 2 π da integral e fazer a distributiva:

= 2 π ∫ 0 1 2 - r 2 ∙ r - r 2 d r =

E podemos abrir em duas integrais:

= 2 π ∫ 0 1 2 - r 2 ∙ r d r + 2 π ∫ 0 1 r 2 d r =

Pra primeira integral, vamos fazer a substituição u = 2 - r 2 :

d u = - 2 r d r ⇒ r d r = - 1 2 d u

u 0 = 2

u 1 = 1

E a integral fica assim:

= 2 π ∫ 2 1 u ∙ - 1 2 d u + 2 π ∫ 0 1 r 2 d r =

Podemos tirar o 1 2 da integral e o “ - ” inverte os limites de integração:

= π ∫ 1 2 u d u + 2 π ∫ 0 1 r 2 d r =

Como u = u 1 2 , e sua primitiva é:

u 3 2 3 2 = 2 3 u 3 2 = 2 3 u u

Então:

= π 2 3 u u 1 2 + 2 π r 3 3 0 1 =

= π 2 3 ∙ 2 ∙ 2 - 2 3 + 2 π 1 3 - 0 =

Podemos colocar π 3 em evidência:

= π 3 4 2 - 2 - 2 = π 3 4 2 - 4

Então achamos o volume:

V W = 4 π 3 2 - 1

Resposta

∫ 0 2 π ∫ 0 1 ∫ r 2 - r 2 r d z d r d θ = 4 π 2 - 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Marque o ponto cujas coordenadas esféricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 2 ,π / 2 ,π / 2 ) ( 4 , -π / 4 ,π / 3 )
Utilize coordenadas esféricas.Calcule ∭ E ( x e x 2 + y 2 + z 2 ) d V , onde E é a porção da bola unitáriax 2 + y 2 + z 2 ≤ 1 que fica no primeiro octante.
Calcule a integral, transformando para coordenadas esféricas. ∫ - 2 2 ∫ - 4 2 - y 2 4 2 - y 2 ∫ - 4 2 - y 2 - x 2 4 2 - y 2 - x 2 x 2 + y 2 + z 2 3 2 d z d x d y
Utilize coordenadas esféricas.Calcule ∭ E ( x 2 + y 2 ) d V , onde E está entre as esferas x 2 + y 2 + z 2 = 4 e x 2 + y 2 + z 2 = 9 ;
Mude de coordenadas retangulares para esféricas. ( 0 , - 2,0 ) ( - 1,1 , - 2 )