Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 4a

∭_W^() z d x d y d z , o n d e W = {(x , y , z) in R^3,x^2 + y^2 + z^2 <= 1 , z >= 0 , x^2 + y^2 >= (1)/(4)} .

Passo 1

Opa, falae, vamo resolver essa questão!

Nós queremos integrar na região W, mas que região é essa?! Vamos primeiro fazer um esboço dessa região.

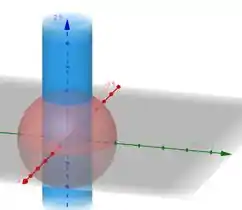
Temos em azul um cilindro, que é dado por x^2 + y^2 = (1)/(4) , e em vermelho a esfera dada por x^2 + y^2 + z^2 = 1 . Cara, a nossa região W está compreendida entre esse cilindro e entre a esfera, mas somente a parte positiva, pois z >= 0 .

Passo 2

Okay, agora que sabemos a região em que estamos trabalhando, vamos aplicar uma mudança de variáveis para ficar mais tranquilo. Vamos utilizar as coordenadas cilíndricas, daí:

{[[x = r cos theta],[y = r sen theta],[z = z]])

Lembrando que o jacobiano das coordenadas cilíndricas é dado por |J| = r .

Agora temos que ter nossos intervalos de integração.

Note que:

x^2 + y^2 + z^2 = 1 -> z^2 = 1 - ( x^2 + y^2 )

z^2 = 1 - (r^2 (sen^2 theta + cos^2 theta))

z^2 = 1 - r^2 -> z = sqrt(( 1 - r^2 ))

Daí, 0 <= z <= sqrt(1 - r^2) .

Cara, pra r vamos ter o seguinte. A nossa região W está indo do nosso cilindro para a nossa esfera, ou seja, do raio do cilindro para o raio da esfera, assim (1)/(2) <= r <= 1 .

Agora pra theta , temos que nossa região ocupa todos os quadrantes do plano, ela da uma volta em torno do eixo y, dai 0 <= theta <= 2 pi .

Passo 3

Vamos então calcular a nossa integral

∭_W^() z d x d y d z = int_0^(2 pi) int_((1)/(2))^1 int_0^(sqrt(1 - r^2)) z r d z d r d theta = int_0^(2 pi) int_((1)/(2))^1 (r - r^3)/(2) d r d theta = (1)/(2) int_0^(2 pi) (9)/(64) d theta = (9 pi)/(64)

Resposta

O resultado da integral é (9 pi)/(64) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize coordenadas cilíndricas.Calcule ∭ E y d V , onde E é o sólido que está entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 4 , acima do plano x y e abaixo do plano z = x + 2 .
Mude de coordenadas retangulares para cilíndricas. ( 1 ,- 1 ,4 ) ( - 1 ,- 3 , 2 )
Identifique a superfície cuja equação é dada.2 r^2 + z^2 = 1
Identifique a superfície cuja equação é dada. z = 4 - r 2
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )