Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 7

7. y = x^2 , y = x^3

Passo 1

Como o enunciado me fornece uma f ( x ) e estamos integrando em relação a y, precisamos encontrar uma f ( y ) .

f_1 (x) = x^2

f_2 (x) = x^3

f_1 (y) = y^((1)/(2))

f_2 (y) = y^((1)/(3))

O gráfico dessa equação é o seguinte:

No eixo x temos: 0 <= x <= 1

No eixo y temos: 0 <= y <= 1

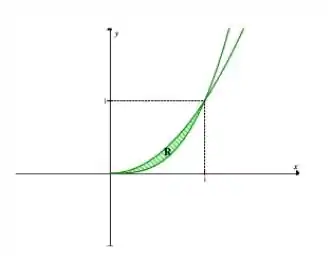
Como podemos observar, temos um anel circular, com raio externo x^3 e raio interno x^2 . Temos a área da seção transversal subtraindo a área do círculo interno da área do círculo externo.

A (y) = pi (f_2 (y) - f_1 (y))

Passo 2

Para obtermos o volume gerado pela revolução de R em torno do eixo y, usaremos a seguinte formula:

V = pi int_a^b [A (y)]^2 d y

Passo 3

Portanto, o volume é:

V = int_0^1 pi (y^((1)/(3)))^2 - pi (y^((1)/(2)))^2 d y

= pi int_0^1 y^((2)/(3)) - y d y

(pi ((y^((5)/(3)))/((5)/(3)) - (y^2)/(2))|_0^1 =

= pi ((3)/(5) - (1)/(2))

= (pi)/(10) u . v .

Resposta

(pi)/(10) u . v .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9 - Determine o volume do sólido gerado pela rotação da região limitada à esquerda pela parábola x = y 2 + 1 e à direita pela reta x = 5 em torno:Do eixo xDo eixo yDa reta x = 5
Ache o comprimento do arco da curva y = ln sec x dex = 0 a x = (pi)/(4)
Volume do hemisfério . Deduza a fórmula V = 2 3 π R 3 para o volume de um hemisfério de raio R comparando suas seções tranversáveis com as de um cilindro sólido circular reto de raio R e altura R , do
R limitada pelos gráficos de y = f x0 , x = a0 , x = ba e y = 0 . Se o volume do solido formado pela revolução de R em torno do eixo x for 4 π e o volume do sólido formado pela revolução de R em torno
Uma tigela hemisférica de raio a contém água a uma profundidade h . Determine o volume de água da tigela.Taxas relacionadas. Água cai em um aquário hemisférico de raio 5 metros a uma taxa de 0,2 m 3 /