Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 08c
Dois carros se movem segundo os seguintes vetores posição:
c ) Em que ponto elas se cruzam?
Passo 1
Para que se cruzes, as posições devem se igualar. Podemos igualar as duas funções vetoriais e verificar quais são os pontos de cruzamento.
Para a primeira função, temos a seguinte desparametrização
E para a segunda função, temos a seguinte desparametrizaçao
Igualando as duas equações
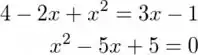
E resolvendo, temos que os pontos que as pistas se cruzam são
Resposta
Exercícios de Livros Relacionados
A velocidade escalar em t = t1.
dois vetores tangentes unitários à trajetória de partícula em t=t 1 . Trace um esboço da trajetória da partícula e represente geometricamente os vetores V t 1 e A t 1 .
dois vetores tangentes unitários à trajetória de partícula em t = t1. Trace um esboço da trajetória da partícula e represente geometricamente os vetores V(t1) e A(t1).
A velocidade escalar em t = t1.
O vetor velocidade v(t).