Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.Revisão - Ex. 45
Dois pontos, e , são diametralmente opostos nas praias de um lago circular com 1 km de diâmetro. Uma pessoa deseja ir do ponto ao ponto . Ela pode remar a uma velocidade de km/h e andar a uma velocidade de km/h. Acha qual o menor tempo gasto para ir de
Até .
Passo 1
Esse vai ser um problema de otimização, (achar o menor tempo). A primeira coisa a tentar se fazer neste tipo de questão é um esboço do que está acontecendo, olhem na imagem abaixo como facilita o entendimento.
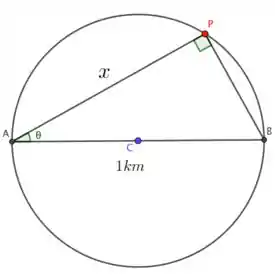
Vamos supor que uma pessoa vai de ao ponto sendo esses pontos diametralmente opostos, ok? Essa pessoa pode remar e também pode andar. Remando ela pode “cortar caminho” e andando tem que ser pela circunferência. Então vamos supor que ela irá remar de até e andar de até , poderia ser o contrário também.
Como vocês podem ver na figura acima, formamos justamente um triângulo retângulo, pois rad é um ângulo inscrito, ou seja, é metade da medida do arco correspondente, que é rad.
Passo 2
Vamos achar agora a expressão que dá o tempo de percurso, lembre-se que tempo é a distância percorrida dividida pela velocidade. Observando na figura anterior, o tempo de percurso pode ser dado por .
Onde tempo remando e tempo andando. E podemos escrever o seguinte
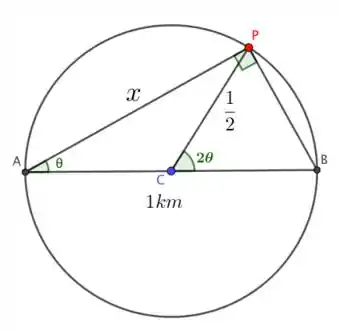
Como vocês viram, agora vamos precisar achar o comprimento do arco .
Passo 3
Temos da figura acima que o ângulo , pois é ângulo central com ângulo inscrito sendo , ou seja,
Sabemos também que a medida do comprimento de um arco é dada pelo seu ângulo central em radiano vezes o valor do raio. Então o valor do comprimento do arco é dado por:
Lembre-se que a circunferência tem diametro , então seu raio é .
Podemos concluir também que , sendo assim:
E temos que o comprimento do arco é .
Passo 4
Agora vamos voltar na fórmula do tempo de percurso:
Comprimento de é e a velocidade nadando é km/h. O comprimento do arco é e a velocidade andando é km/h. Sendo assim,
É a fórmula que nos dá o tempo de percurso com , pois o comprimento de é menor ou igual ao diâmetro.
Passo 5
Utilizando a fórmula anterior, nós vamos derivar a função duas vezes para ver como ela se comporta:
Aqui usamos .
Acima foi utilizada a derivada de para com a regra da cadeia.
É importante que vocês percebam que para todo e isso indica que a nossa função tem concavidade para baixo em todo esse intervalo. É importante entender que neste caso o mínimo absoluto ocorrerá em algum extremo do intervalo, ok? Acontece algo como abaixo:
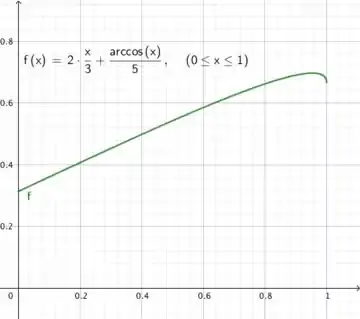
Passo 6
Agora testamos os extremos do intervalo e para ver qual deles leva ao menor valor de .
e
Temos que . Logo, o menor tempo gasto para ir de Até é horas. Ele vai totalmente a pé, pois . Bacana, né?
Resposta
Menor tempo gasto horas.