Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 82

Duas fontes de luz de igual potência estão colocadas a 10   m uma da outra. Um objeto deve ser colocado em um ponto P   sobre uma reta l paralela à reta que une as fontes de luz a uma distância d   metros dela (veja a figura). Queremos localizar   P   em l de forma que a intensidade de iluminação seja minimizada. Precisamos usar o fato de que a intensidade de iluminação para uma única fonte é diretamente proporcional à potência da fonte e inversamente proporcional ao quadrado da distância da fonte.

(a) Encontre uma expressão para a intensidade I ( x ) em um ponto   P .

(b) Se d = 5   m , use os gráficos de   I ( x )   e   I ' ( x )   para mostrar que a intensidade é minimizada quando x = 5   m , isto é, quando   P está no ponto médio de l .

(c) Se d = 10   m , mostre que a intensidade (talvez surpreendentemente) não é minimizada no ponto médio.

(d) Em algum ponto entre d = 5   m e d = 10   m existe um valor de d   no qual o ponto de iluminação mínima muda abruptamente. Estime esse valor de d   por métodos gráficos. Encontre então o valor exato de d .

Passo 1

E aí, galerinha!

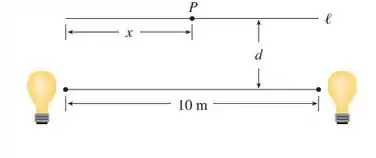
Nesse problema temos duas lâmpadas e um objeto localizado no ponto P como descrito na imagem

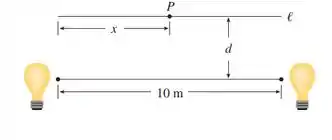
Nosso objetivo é encontrar uma expressão I x da intensidade luminosa no ponto P sabendo que a intensidade é proporcional à potência da fonte sobre a distância ao quadrado.

E também se d = 5   m , temos que plotar os gráficos de   I ( x ) e I ' ( x )   para mostrar que a intensidade é minimizada quando x = 5   m , isto é, quando   P está no ponto médio de l .

Temos tambem que fazer o mesmo para d = 10   m e mostrar que agora o ponto medio de l não é o ponto da menor intensidade.

Por fim, temos que estimar um valor para d entre d = 5   m e d = 10   m em que existe um valor no qual o ponto de iluminação mínima muda abruptamente.

Bastante coisa, não é?

Para resolver esse problema, vamos chamar a potência da fonte de k e a partir da definição

I x = k r 2

Onde r é a distância entre o objeto e a fonte e assim, derivar e igualar a 0 para determinar os pontos de minimização.

Sacou? Bora começar!

Passo 2

Como a intensidade é proporcional a k r 2 ... temos que a intensidade no ponto P será a soma das duas lâmpadas.

I x = I 1 + I 2 = k r 1 2 + k r 2 2

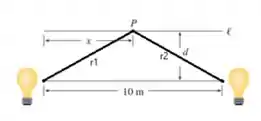
r 1 pode ser escrito como

r 1 = x 2 + d 2

Já r 2 como

r 2 = 10 - x 2 + d 2

Substituindo em I x

I x = k x 2 + d 2 + k 10 - x 2 + d 2

I x = k x 2 + d 2 + k x 2 - 20 x + 100 + d 2

Tranquilo até aqui?

Passo 3

O tamanho da constante k não afetará a localização do ponto de máxima intensidade, então, por conveniência nós vamos usar que k = 1 .

Derivando I x aplicando a regra da cadeia, temos

I ' x = d 1 x 2 + d 2 d x + d 1 x 2 - 20 x + 100 + d 2 d x

I ' x = d x 2 + d 2 d x d 1 u d u + d x 2 - 20 x + 100 + d 2 d x d 1 v d v

I ' x = - 2 x x 2 + d 2 2 - 2 x - 10 x 2 - 20 x + 100 + d 2 2

Substituindo d = 5 em I x e em I ' ( x ) nós temos

I 5 x = 1 x 2 + 25 + 1 x 2 - 20 x + 125

I 5 ' x = - 2 x x 2 + 25 2 - 2 x - 10 x 2 - 20 x + 125 2

Plotando seus gráficos...

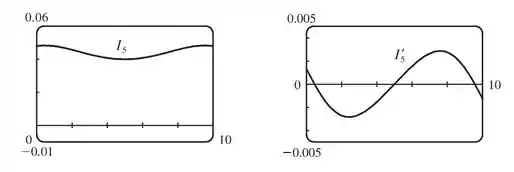
Pelo gráfico parece que I 5 x tem seu mínimo em x = 5 m . O que é confirmado em I 5 ' pois o gráfico corta o eixo x nesse ponto.

Show?

Passo 4

Agora vamos substituir d = 10 em I x e em I ' ( x ) nós temos

I 10 x = 1 x 2 + 100 + 1 x 2 - 20 x + 200

I 5 ' x = - 2 x x 2 + 100 2 - 2 x - 10 x 2 - 20 x + 200 2

Plotando os gráficos...

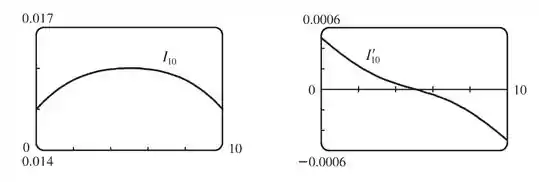
Se analisarmos o gráfico de I 10 ' , poderíamos pensar que em x = 5 m a intensidade teria um valor mínimo. Mas quando analisamos I 10 , vemos que esse ponto na verdade é um máximo da função, onde a intensidade é máxima...

Bacana, não é?

Passo 5

Pelas primeiras figuras nas respostas (b) e (c), vemos que a iluminação mínima muda do ponto média ( x = 5 com d = 5 ) para os pontos extremos, ( x = 0 e x = 10 com d = 10 ), então, se tentarmos d = 6 :

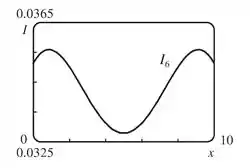
nós vemos que o valor mínimo ainda acontece em x = 5 .

Agora, se tentarmos d = 8 :

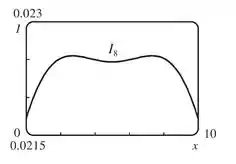
nós temos valores mínimos no ponto médio e nos pontos extremos, então, I 5 deve se igualar a I 0 . Para encontrar esse valor de d , nós resolvemos I 0 = I 5 (com k = 1 ):

1 d 2 + 1 100 + d 2 = 1 25 + d 2 + 1 25 + d 2 = 2 25 + d 2

Simplificando e isolando d em um lado da igualdade, temos

25 + d 2 100 + d 2 + d 2 25 + d 2 = 2 d 2 100 + d 2

2500 + 125 d 2 + d 4 + 25 d 2 + d 4

2500 = 50 d 2

d 2 = 50

d = 5 2 ≈ 7,071   ,   0 ≤ d ≤ 10

A terceira figura, um gráfico de I 0 - I ( 5 ) com d independente, confirma que   I 0 - I 5 = 0 , logo, I 0 = I ( 5 ) , quando d = 5 2 :

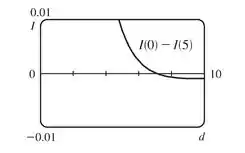
Então, o ponto de menor iluminação muda abruptamente do ponto médio para os pontos extremos quando d = 5 2 .

E fim! O que achou? Responde Aí!

Resposta

  1. I x = k x 2 + d 2 + k x 2 - 20 x + 100 + d 2 .
  2. Resposta nos gráficos.
  3. Resposta nos gráficos.
  4. d = 5 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se movimenta sobre uma reta horizontal, de acordo com a equação s = t 3 - 3 t 2 - 9 t + 2 , onde s cm é a distância orientada da partícula a partir de um ponto O em t s. O sentido positi
Um objeto está escorregando por um plano inclinado de acordo com a equação s = 12 t 2 + 6 t , onde s m é a distância orientada do objeto até o topo do plano, após t s do início do movimento. (a) Ache
Uma bola é atirada para cima do topo de um prédio com 112m de altura. Sua equação de movimento é s = - 16 t 2 + 96 t , onde s m é a distância orientada da bola ao ponto de partida, após t s. Ache (a)
Dada f (x) = (1)/(12) x^4 + (2)/(3) x^3 + (3)/(2) x^2 + 8 x + 2 . Para que valores de xf " ( x )0 ?
Encontre (d^3 y)/(d x^3) se y = sqrt(3 - 2 x) .