Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 3

Encontrando um centroide: encontre um centroide da região do primeiro quadrante delimitado pelo eixo x, a parábola y 2 = 2 x e a reta x + y = 4 .

Passo 1

Faaaala, cara! Tranquileba?

Temos que:

y 2 = 2 x   e   x + y = 4

E analisando o gráfico para o primeiro quadrante, temos:

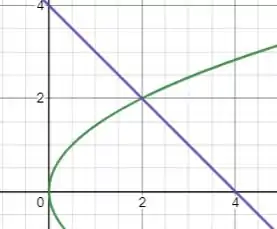
Vemos que y ∈ 0,2 e x ∈ y 2 2 ,   4 - y

E temos que:

x c e n t = ∬ y   d x d y M

E análogo para y c e n t

y c e n t = ∬ x   d x d y M

E para M:

M = ∬ d x d y

Passo 2

Para M:

M = ∫ 0 2 ∫ y 2 2 4 - y d x d y

∫ 0 2 ( x y 2 2 4 - y     d y

∫ 0 2 4 - y - y 2 2 d y

( 4 y 0 2 - 1 2 y 2 0 2 - 1 6 y 3 0 2

M = 14 3

Passo 3

Para x c e n t :

M y = ∫ 0 2 ∫ y 2 2 4 - y x   d x d y

∫ 0 2 ( 1 2 x 2 y 2 2 4 - y d y

1 2 ∫ 0 2 16 - 8 y + y 2 - y 4 4 d y

1 2 16 y 0 2 - 4 y 2 0 2 + 1 3 y 3 0 2 - 1 20 y 5 0 2

M y = 128 15

Para M x :

M x = ∫ 0 2 ∫ y 2 2 4 - x y   d x d y

∫ 0 2 ( y x y 2 2 4 - x   d y

∫ 0 2 y 4 - y - y 2 2 d y

  2 y 2 0 2 - 1 3 y 3 0 2 - 1 8 y 4 0 2

M x = 10 3

Assim, como já dito anteriormente:

x c e n t = M y M

y c e n t = M x M

Logo

x c e n t = 128 15 14 3 = 64 35

E

y c e n t = 10 3 14 3 = 5 7

Resposta

x c e n t = 64 35

E

y c e n t = 5 7

Exercícios de Livros Relacionados

Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O sólido do exercício 19; ρ x , y , z = x 2 + y 2
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O hemisfério x 2 + y 2 + z 2 ≤ 1 ,z ≥ 0 ; ρ x , y , z = x 2
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a 4 k g m 3 . z = x 2 + y 2 z = 9 - x 2 - y 2