Encontre a área da parte da esfera que está dentro do parabolóide .
Passo 1
Oioi pessoal, vamos começar entendendo o que o exercício quer. Bom ele pede para que a gente encontre a área da parte da esfera que está dentro do parabolóide .
Para isso podemos usar a integral dupla que representa a área da superfície:
Bom, então iremos começar achando as derivadas parciais e e depois substituiremos na integral.
Depois iremos parametrizar em coordenadas polares para ficar mais fácil de achar os limites de integração .
Feito isso, é só pôr a mão na massa e resolver a conta.
Vamos começar!
Passo 2
Vamos achar quem são essas derivadas parciais e . Ish, mas você percebeu que temos que ter uma equação para ? Bom isso não será um problema , temos que isolar o .
Podemos ajustar a equação somando dos dois lados de forma que podemos escrever em forma de produto notável.
Somando:
E isso é a mesma coisa que
Agora vamos passar tudo para o outro lado:
Passando o expoente em forma de raiz:
Show, agora temos uma equação de .
Passo 3
Agora sabemos que , vamos achar as derivadas parciais.
Começando por :
Aí a gente vai usar uma regrinha da cadeia e vamos ficar com:
Então temos que
Agora para
E pra é basicamente a mesma coisa hehe, só que em relação a
Nosso resultado final fica:
Vamos substituir na nossa integral:
Ficaremos com:
Passo 4
Shoow agora a gente pode mandar isso pra nossa integral
Vamos elevar as derivadas parciais ao quadrado:
Se ajeitarmos essa integral feiosa, ficamos com
Passo 5
Beleza galera, agora precisamos passar tudo para coordenadas polares:
e
Esse valor é sempre o mesmo para coordenadas polares mas achamos através da fórmula:
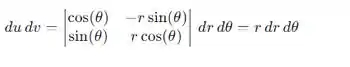
Substituindo os novos valores na integral:
teremos:
Parece assustador, porém olha só esse bizu.Normalmente quando temos em um mesmo problema podemos tentar juntá los de tal forma para substituir por .
Sendo assim:
Logo:
Olha quem apareceu ali, dessa forma:
Passo 6
Show, mas ainda precisamos achar nossos limites de integração
O de é tranquilinho, como o enunciado não dá nenhuma restrição ele dá a volta completa no eixo , então nós temos que
Já o de a gente vai precisar de um jeitinho especial para achar.
Lembra que a nossa esfera está dentro do parabolóide ??
Isso quer dizer que precisamos encontrar o valor de acordo com o parabolóide. Vamos ver graficamente só para você sacar o que eu estou falando.
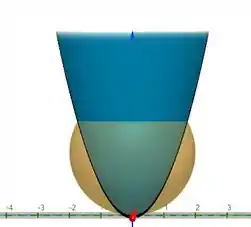
Queremos achar a área que corresponde a parte que está verde , e os nossos limites de integração será a parte pretinha, entendeu?
Para a gente encontrar esse valor teremos que igualar nossas duas funções, temos que
e que
então podemos dizer que:
Então chegamos que
ou
Só que quem é mesmo?
Que nas nossas coordenadas polares é a mesma coisa que
Logo:
Então uhul achamos nossos limites
Passo 7
Agora vamos resolvê-la:
Separando as raízes:
Logo:
Sempre começamos pela ordem de dentro para fora, ou seja, vamos integral primeiro em relação a :
Vamos fazer uma substituição simples e chamar
Substituindo na integral:
logo:
Retornando com :
Logo:
2
Substituindo em:
teremos:
Passo 8
Agora para fechar vamos resolver:
Logo: