Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 55
(a) Use a Regra do Ponto Médio para integrais duplas (veja a Seção ) com seis quadrados para estimar a área da superfície .
(b) Use um sistema de computação algébrica para aproximar a área de superfície da parte (a) até a quarta casa decimal. Compare com sua resposta para a parte (a).
Passo 1
Fala, galera! Beleza? 😊
No item (a), iremos resolver a área de superfície
Através da Regra do Ponto Médio para integrais duplas, definidas por
Iremos usar fórmulas para cada coisinha dessa questão.
E no item (b), usar softwares para expressar os valores do item (a) em até quatro casas decimais, show?
Passo 2
(a) Pessoal, primeiro vamos expressar a área da superfície como uma integral através dessa fórmula aqui:
Vamos fazer as derivadas parciais da função dada na questão e substituir na raiz:
Temos nossos limites de integração também já definidos no enunciado, com
Portanto, jogando tudo na fórmula, teremos:
Organizando, chegaremos a
Ou melhor,
Passo 3
Agora vamos usar a regra do Ponto Médio, com a fórmula
Onde
E e são subquadrados em cada eixo, como podemos ver abaixo, com e :
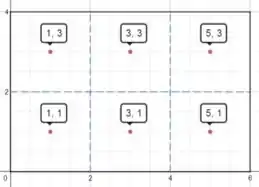
E em cada quadradinho temos os pontos médios .
Lembrando que a área de cada subquadrado é dado por
Com isso, podemos fazer que a ��rea de superfície é dada por:
Substituindo cada valor dentro da função , teremos:
Passo 4
(b) Agora, se usarmos um sistema de computação algébrica para aproximar a mesma integral, obteremos:
Repare que a Regra do Ponto Médio nos deu uma aproximação bastante coerente da área da superfície, mas para uma maior precisão, deveria se usar mais quadrados.