Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 26
Encontre a área da região que está dentro da primeira curva e fora da segunda curva:
Passo 1
Olá, meu amigo. Vamos de resolução.
Aqui a gente tem as curvas parametrizadas:
E precisamos encontrar a área entre uma curva e outra. A melhor forma de a gente fazer isso é primeiro ver como estão as nossas duas curvas, assim a gente vai obter a melhor estratégia de resolução para a nossa situação.
A região procurada é dada por:
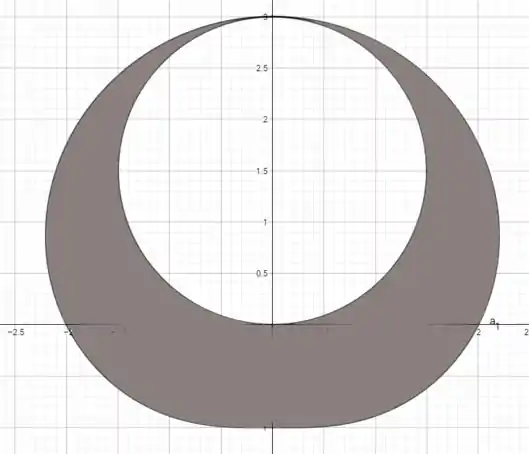
Geramos esse gráfico com ajudar do GeoGebra.
Lembrando que como estamos utilizando coordenadas polares os valores de são positivos.
A área é dada por:
Mas veja que aqui a gente tem uma área maior, a mais externa, e se a gente subtrair a área do círculo interno, a gente vai ter a área que a gente precisa.
Veja abaixo, que para percorremos toda a nossa figura, deveremos partir da origem, e ‘varrer’ em sentido anti-horário de até o ângulo , dessa forma, esse é o nosso intervalo de integração.
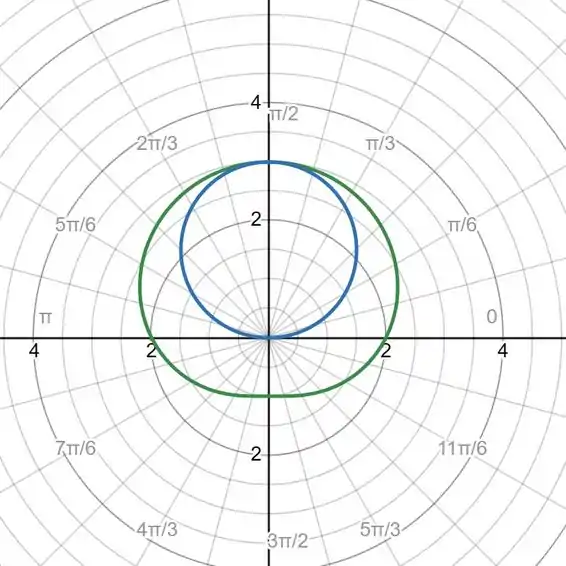
Passo 2
Para encontrarmos a área desejada, calcularemos a área abaixo da curva e retiraremos a área da curva .
Fazendo , temos que logo:
Porém , dessa forma, temos:
Completando o quadrado, isso é, iremos organizar o termo de forma a ter ele em produtos notáveis:
Reconhecemos essa curva como um círculo de raio , dessa forma, sua área é dada por
Passo 3
Para calcular a área abaixo de , lembramos que:
Substituindo:
Podemos separar em 3 integrais:
A primeira integral é dada por:
A segunda integral é dada por:
Já na terceira temos:
Utilizando da identidade trigonométrica:
Dividindo a integral em duas:
Vamos então aos cálculos das integrais:
Calculando:
Então é:
Assim, a área procurada é a subtração dessas 2 áreas, ou seja:
E aqui a gente termina a nossa resolução. Forte abraço e até uma próxima.
Resposta
A área da seção é .