Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 13
Encontre a área da superfície com precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora para estimar a integral.
A parte da superfície que está acima do disco .
Passo 1
Fala, galerinha! Tudo belê?
Nesse exercício, precisamos encontrar a área de parte da superfície definida por
Que fica acima do disco
Cujo resultado deve ter precisão de quatro casas decimais expressando a área em termos de uma integral simples e usando uma calculadora pra estimar a integral (ou seja, iremos usar a integral para definir a área).
A figura a seguir esquematiza a região delimitada pela superfície e pelo disco:
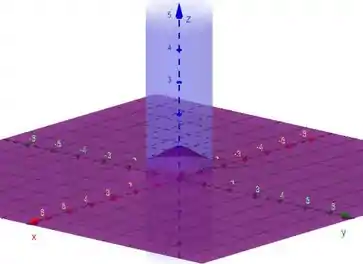
Pra gente encontrar essa área, usaremos essa fórmula aqui:
Iremos encontrar logo os limites de integração dessa região , as derivadas e e jogar na fórmula. Show?
Passo 2
Para encontrar os limites de integración, começaremos com a equação do disco. Sabemos que a região de integração será delimitada por uma circunferência completa com raio variando de 0 a 1, já que
Agora iremos analisar
Fazendo as derivadas em relação a e , então
Sendo assim, a área da superfície pode ser escrita como:
Conforme visto no passo 1, a região fornecida no enunciado é delimitada por um círculo, sendo assim, podemos mudar o sistema de coordenadas cartesianas para polar, com
Fazendo isso, temos:
Organizando, teremos no numerador dentro da raiz:
Fazendo um M.M.C. com os termos dentro da raiz, chegaremos a
Passo 3
Podemos usar uma estratégia para calcular essa integral, dividindo ela em partes e resolvendo cada termo com seus integrandos, dessa forma aqui:
Resolvendo a integral obtida, teremos:
Nesse ponto, reduzimos a área da superfície pedida a uma integral simples (como pedia o enunciado), e calculando o valor dessa integral através de uma calculadora obtemos o seguinte resultado:
Show de bola demais, gente! 😊