Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 37
Calcule a integral tripla usando apenas interpretação geométrica e simetria.
, onde é a região cilíndrica , .
Passo 1
Fala, galera! Beleza?
Nessa questão, precisamos calcular uma integral tripla, mas sem integrar... vamos usar só interpretação geométrica e simetria.
Na interpretação geométrica, vamos precisar calcular o volume da nossa região, que é um cilindro. Então pra isso, vamos relembrar a fórmula do volume de um cilindro:
Pra analisarmos essa integral por simetria, temos que ver as funções com paridade:
- Funções ímpares, , têm a propriedade que:
- Funções pares, , têm a propriedade que
Percebe que podemos usar essas propriedades de paridade de funções quando temos regiões simétricas (por isso falamos de simetria).
Nessa questão específica, a gente vai começar separando nossa integral em duas, pra ficar mais fácil de analisarmos a simetria e geometria da região:
Agora vamos ver cada uma dessas integrais separadamente.
Passo 2
A primeira integral:
Como o integrando é uma constante, ele pode sair da integral e fica:
E agora essa integral representa exatamente o volume da nossa região, já que:
Ou seja,
Bom, a região é um cilindro:
Com entre e .
Pra facilitar o cálculo do volume, vamos ver o desenho dele:
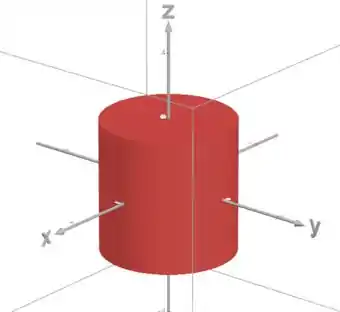
Calculando o volume:
Nesse caso, a base é um círculo de raio :
E a altura é a distância de até :
Então:
E:
Passo 3
Por último, vamos ver a segunda integral:
Como agora nosso integrando não é uma constante, vamos analisar a paridade das funções que aparecem:
e são funções pares:
é uma fun��ão ímpar:
Vamos focar na variável .
Percebe que se a gente voltar pro desenho, a gente vê que a nossa região é simétrica em :
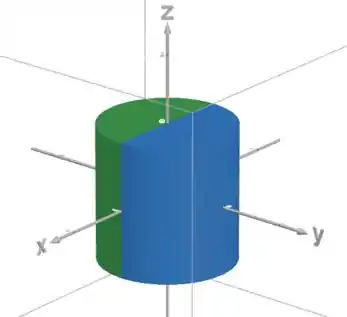
A região verde () é igual a região azul () só que espelhada.
Então podemos aplicar o fato que olhando por , a integral vai dar zero!
Lembra que pra uma função ímpar:
Agora, se quando integrarmos em função de a integral vai ser , não importa quando vai dar a integral das outras variáveis! No final:
E então: