Encontre as assíntotas horizontais e verticais:
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos encontrar as assíntotas verticais e horizontais da função.
Mas o que são as assíntotas??
Bom... uma reta é chamada de assíntota horizontal da curva se
ou
Em outras palaras, quando tomamos o limite ao infinito da função, e encontramos um valor , este valor é a assíntota horizontal da função.
Para a assíntota vertical é um pouco parecido também pois se trata de uma reta (mas na vertical haha).
Para encontrar a assíntota vertical é muito simples: devemos pensar o seguinte “Para que ponto que quando se aproxima a função ‘explode’ para infinito”?? (podem ser um ou mais pontos).
Agora bora lá!! 😉
Passo 2
Para encontrar a assíntota horizontal, tomaremos o limite da função quando .
Primeiro iremos dividir os termos pela variável de maior grau, para que possarmos ‘cortar’ alguns termos ao fazer
Multiplicando o numerador e o denominador por , temos:
Simplificando, obtemos:
Logo, não tem assíntota horizontal :D
Passo 3
Para encontrar a assíntota vertical é muito simples, devemos pensar o seguinte “Para que ponto que quando se aproxima a função ‘explode’ para infinito” (podem ser um ou mais pontos), ou seja:
Porém, para facilitar, iremos “brincar” com a equaç��o, para isso, seja
Agora encontrando as raízes da equação no denominador, podemos simplifica-lo, daí ficamos com
Então reescrevemos o limite como sendo
Para a condição de assíntota é satisfeita, pois quando mais próximo de é o denominador, maior será o numerador, ou seja, , ocorre quando , logo é uma assíntota vertical.
Note que os valores de são calculados igualando o denominador a e encontrando os valores de .
Passo 4
Mostraremos agora, uma comprovação gráfica do resultado obtido
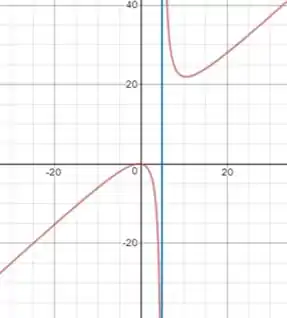
Perceba que a assíntota vertical é dada pela reta azul passando em .
Resposta
Não tem assíntotal horizontal
é uma assíntota vertical