Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.6 - Ex. 39
Encontre as assíntotas horizontal e vertical de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.
Passo 1
Opa, bora lá! Temos que achar as assíntotas da curva:
Para acharmos as assíntotas, nós temos métodos particulares, para acharmos a horizontal é diferente para achar a vertical, porém as duas tem em vão ter algo a ver com infinito, então vamos começar!
Passo 2
Começaremos com a assíntota horizontal, temos que fazer:
Se der um número real, a assíntota será esse número, caso dê infinito. Não teremos assíntota horizontal. Vamos para o cálculo!
Reduzindo o com o e colocando o limite em todas as parcelas, temos:
Substituindo tudo para dentro do limite, temos isso aqui:
Então, não temos assíntota horizontal para positivo. Faremos a mesma coisa para :
Reduzindo o com o e colocando o limite em todas as parcelas, temos:
Botando para dentro da expressão do limite, temos:
Então, não temos assíntota horizontal para negativo.
Passo 3
Agora, partiremos para a assíntota vertical, como fazemos para calcular?
Temos primeiramente que ver os valores de na qual a função não existe, para essa função da questão são os valores que anular o denominar.
Os valores de que anulam o denominador e :
Faremos os limites de tendendo a esses valores e se der infinito, então a reta , no caso do ponto e igualmente para Ficou confuso? Vamos fazer as contas e aí você entenderá melhor:
Temos sempre que fazer o limite à esquerda e direita do ponto ( os chamados limites laterais).
Começaremos por
Temos que para e próximo de :
é negativo
é negativo.
Então para pontos à direita de :
Para
é negativo
é positivo
Então para pontos à esquerda de :
A reta é assíntota vertical.
Faremos agora para :
Temos que para e próximo de -2:
é negativo
é negativo.
Então para pontos à direita de :
Para e próximo de 2:
é negativo
é positivo.
Então para pontos à esquerda de :
A reta é assíntota vertical.
Passo 4
Agora a gente vai plotar o gráfico:
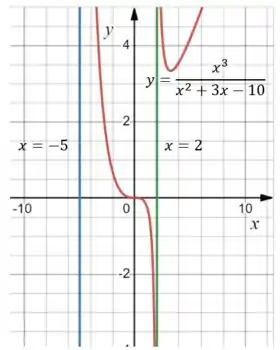
Como a gente previu, não temos assíntotas horizontais e as assíntotas verticais estão de vermelho e azul!
Resposta
São as assíntotas verticais.