Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 15
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento , se a densidade em qualquer ponto for proporcional ao quadrado da sua distância ao vértice oposto à hipotenusa.
Passo 1
Fala pessoal, tudo bem com vocês?
Nesse exercício precisamos encontrar o centro de massa de um triangulo retângulo isósceles que tem lados iguais de comprimento a. Sabemos também que a densidade em qualquer ponto é proporcional ao quadrado da distância do vértice à hipotenusa.
O primeiro passo é desenharmos tudo isso que acabamos de ler, e compreender nossa figura. Veja a imagem a seguir:
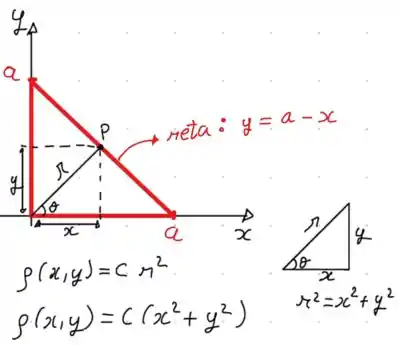
Observe que conseguimos escrever a densidade em função de e aplicando Pitágoras no triangulo retângulo.
Não se preocupe com a constante , no fim você vai ver que o centro de massa não depende dela. Essa constante escrevemos de forma genérica, ela pode assumir qualquer valor maior que zero, inclusive .
Sabendo dessas informações, vamos lembrar como se calcula centro de massa. Sabemos que a massa e os centro de massas , são obtidos através das seguintes fórmulas:
Onde,
Um detalhe muito importante, a região , e a área formada pelo triângulo da figura acima. Repare bem na figura, e vê se você concorda que podemos fazer as seguintes variações de intervalo de integração:
Lembre-se, sempre que temos um intervalo variando em forma de função, esse deve ser integrado primeiro.
Com esses bizu é começar a calcular! Comece determinando a massa e depois encontre o centro de massa!
Vamos nessa turma!
Passo 2
Primeiro vamos determinar nossa densidade, pois ela é crucial na determinação da massa.
Como vimos no passo , ao esboçar nossa região conseguimos achar a seguinte expressão para a densidade:
Sabendo disso, podemos calcular a massa:
Nossa região , também vimos que pode ser expressa por:
Como temos um triangulo, percebemos que no eixo ele pode variar de até , e no eixo , podemos variar de 0 até a reta que une os vértices do triangulo.
Agora, vamos substituir na integral. Ficamos com:
Passo 3
Bom, agora vamos integrar.
Assim, integrando em temos:
Aplicando os limites de integração, temos:
Agora vamos integrar em . Integrando ficamos com:
Aplicando os limites, temos que:
Assim, concluímos que a massa é:
Passo 4
Agora vamos determinar os centros de massa:
Lembrando que:
Vamos começar por . Substituindo os valores temos que:
Simplificando um pouco, temos:
Integrando em primeiro. Vamos ter:
Aplicando os limites de integração, temos:
Simplificando passo a passo, ficamos com:
Passo 5
Integrando em , temos:
Aplicando os limites de integração, vamos ter:
Colocando em evidencia e simplificando com o do denominador, temos:
Logo, o centro de massa em relação a é:
Passo 6
Agora precisamos determinar o centro de massa em relação a .
O processo vai ser o mesmo que fizemos para .
Substituindo os valores em , vamos ter:
Simplificando um pouco, ficamos com:
Integrando em , vamos ter:
Aplicando os intervalos de integração, obtemos:
Passo 7
Agora, devemos integrar em . Mas antes vamos simplificar o máximo possível essa expressão. Assim:
Assim, já facilita a integral. Agora vamos separar em duas integrais:
Na primeira integral não tem segredo, é só integrar cada termos . Já na segunda, a gente não a expandiu, porque podemos aplicar uma substituição do tipo:
Substituindo, temos:
Integrando e voltando para a variável , temos:
Aplicando os intervalos de integração, temos:
Novamente, colocando em evidencia e simplificando com o denominador vamos ter:
Logo, obtemos como resposta:
Por causa da simetria, teremos que: