Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.5 - Ex. 13
Determine o centro de massa da lâmina com formato de triângulo reto isósceles com lados iguais de tamanho se a densidade em qualquer ponto for proporcional ao quadrado da distância do ponto ao vértice oposto à hipotenusa.
Passo 1
E aí, galera! Tudo em ordem?
A questão pede para acharmos o centro de massa da lâmina com formato de triângulo reto isósceles com lados , onde a densidade é a distância ao quadrado de um ponto ao vértice oposto à hipotenusa do triângulo.
O centro de massa é um ponto com coordenada:
E o valor dessas coordenas a gente consegue calculando as seguintes integrais duplas:
Aqui, nossa variável se refere a massa dessa lâmina, que a gente vai precisar calcular pela integral:
Então, vamos usar a descrição da lâmina para encontrar nossos limites de integração das nossas integrais, resolver a integral da massa para finalmente conseguirmos substituir nas integrais de e para calculá-las.
Bora lá!
Passo 2
Vamos começar traçando nossa região de integração , que aqui é a própria superfície da lâmina. O enunciado diz que nosso triângulo é:
- Reto: então ele tem um ângulo de .
- Isósceles: então ele tem dois lados iguais.
- Medida dos lados sendo .
Então temos o seguinte triângulo, que a gente pode colocar com um vértice na origem pra facilitar a definição dos limites em e :
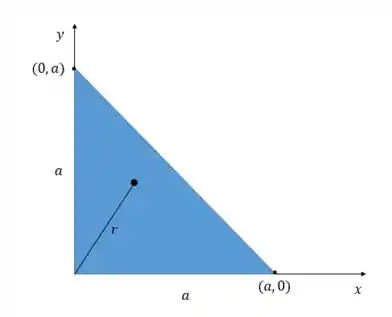
Temos que nossa densidade é proporcional à distância ao quadrado do ponto até o vértice oposto a hipotenusa. Como essa distância é , nossa densidade é dada por:
Onde é uma constante de proporcionalidade.
Como a distância de um ponto até a origem é dada por:
Elevando a equação ao quadrado, podemos escrever através da relação
Assim, substituindo na densidade, temos que:
Precisamos agora descobrir como e variam. Mantendo fixo e variando , temos que
E a reta que limita superiormente será a reta da hipotenusa, dada por
Passo 3
Vamos começar calculando a integral da massa . Com os limites de integração que acabamos de encontrar, ficamos com:
Tirando a constante para fora, resolvemos primeiro a integral de dentro em relação a , tratando como constante:
Aplicando os limites de integração:
Resolvendo a integral que sobrou:
Por fim, aplicando os limites de integração, temos que:
Passo 4
Agora que temos a massa e nossos limites de integração, podemos calcular o que estamos procurando: e .
Observando a simetria do problema, temos que as distâncias em e em são as mesmas, logo, pela simetria do problema, vemos que . Calculando então a posição do centro de massa, temos que:
Começando pela integral “de dentro” e aplicando os limites de integração:
Agora resolvemos a integral que nos restou:
Aplicando os limites de integração:
Substituindo o valor de que encontramos no passo 3:
Finalmente chegamos em:
Então as coordenadas do nosso centro de massa são: