Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.5 - Ex. 9

Determine a massa e o centro de massa da lâmina que ocupa a região D e tem função densidade ρ .

D é delimitada pela parábola x = y 2 e pela reta y = x - 2 ; ρ x , y = 3 .

Passo 1

Faala, pessoal!

Essa questão pediu pra gente calcular duas coisas: a massa e o centro de massa de uma lâmina...

Vamos relembrar as fórmulas disso.

Em uma lâmina de densidade ρ x , y em uma região D , a massa vale

m = ∬ D ρ x , y d A

Já as coordenadas do centro de massa são:

x - = 1 m ∙ ∬ D x ∙ ρ x , y d A

y - = 1 m ∙ ∬ D y ∙ ρ x , y d A

Então pra gente resolver isso, vamos começar olhando pra região que a lâmina ocupa ( D ), que é o domínio das nossas integrais. Ai vamos definir os limites de integração.

Depois, calculamos a massa pela integral (tem que ser a primeira coisa a calcular, porque o centro de massa depende dela).

E por último calculamos x - e y - pelas integrais.

Passo 2

Vamos olhar para o domínio D .

Ele está entre uma parábola e uma reta:

x = y 2

y = x - 2 ⇒ x = y + 2

Se a gente fizer um sistema, achamos os pontos de interseção entre essas duas curvas:

x = y 2 x = y + 2

Igualando o x das duas equações:

y 2 = y + 2

y 2 - y - 2 = 0

Por Bhaskara:

y = 1 ± 1 + 8 2 = 1 ± 3 2

y 1 = 2 ⇒ x 1 = 4 y 2 = - 1 ⇒ x 2 = 1

Agora que já sabemos os pontos de interseção, podemos desenhar as curvas:

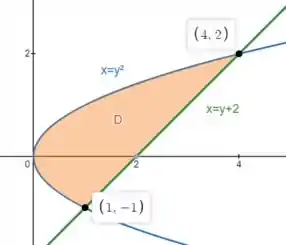
Nosso domínio pode ser descrito com y entre - 1 e 2 , e x entre as duas curvas:

- 1 ≤ y ≤ 2

y 2 ≤ x ≤ y + 2

Passo 3

Agora vamos aplicar os limites de D na fórmula da massa:

m = ∬ D ρ x , y d A

Como ρ x , y = 3 , a integral fica:

m = ∫ - 1 2 ∫ y 2 y + 2 3 d x d y

Integramos sempre de dentro pra fora. Então primeiro em função de x , considerando y constante:

∫ - 1 2 ∫ y 2 y + 2 3 d x d y =

= ∫ - 1 2 3 x y 2 y + 2 d y =

Aplicando os limites de integração:

= ∫ - 1 2 3 y + 2 - 3 y 2 d y =

= ∫ - 1 2 3 y + 6 - 3 y 2 d y =

Agora integramos em função de y :

= 3 y 2 2 + 6 y - 3 y 3 3 - 1 2 =

= 3 ∙ 2 2 2 + 6 ∙ 2 - 2 3 - 3 ∙ - 1 2 2 + 6 ∙ - 1 - - 1 3 =

Então:

= 6 + 12 - 8 - 3 2 - 6 + 1 =

= 10 + 7 2 ⇒ m = 27 2

Passo 4

Agora vamos calcular a posição do x do centro de massa. A fórmula é:

x - = 1 m ∙ ∬ D x ∙ ρ x , y d A

x - = 2 27 ∙ ∫ - 1 2 ∫ y 2 y + 2 3 x d x d y

Vamos integrar de dentro pra fora. Primeiro em função de x , com y constante:

2 27 ∙ ∫ - 1 2 ∫ y 2 y + 2 3 x d x d y =

= 2 27 ∙ ∫ - 1 2 3 x 2 2 y 2 y + 2 d y =

Aplicando nos limites de integração:

= 2 27 ∙ ∫ - 1 2 3 2 y + 2 2 - 3 2 y 2 2 d y =

Podemos colocar 3 2 em evidência e tirar da integral, e abrir os quadrados:

= 2 27 ∙ 3 2 ∙ ∫ - 1 2 y 2 + 4 y + 4 - y 4 d y =

= 1 9 ∙ ∫ - 1 2 - y 4 + y 2 + 4 y + 4 d y =

Agora integramos em função de y :

= 1 9 ∙ - y 5 5 + y 3 3 + 4 y 2 2 + 4 y - 1 2 =

= 1 9 ∙ - 2 5 5 + 2 3 3 + 2 ∙ 2 2 + 4 ∙ 2

- - - 1 5 5 + - 1 3 3 + 2 ∙ - 1 2 + 4 ∙ - 1 =

Resolvendo as contas:

= 1 9 ∙ - 32 5 + 8 3 + 8 + 8 - 1 5 + 1 3 - 2 + 4 =

= 1 9 ∙ - 33 5 + 9 3 + 18 =

Vamos colocar esses termos dentro dos parênteses no mesmo denominador:

= 1 9 ∙ - 33 5 + 3 + 18 =

= 1 9 ∙ - 33 + 15 + 90 5 = 72 45

Então,

x - = 8 5

Passo 5

Para calcular a posição do y do centro de massa, vamos fazer o mesmo processo. A fórmula é:

y - = 1 m ∙ ∬ D y ∙ ρ x , y d A

y - = 2 27 ∙ ∫ - 1 2 ∫ y 2 y + 2 3 y d x d y

Vamos integrar de dentro pra fora. Primeiro em função de x , com y constante:

2 27 ∙ ∫ - 1 2 ∫ y 2 y + 2 3 y d x d y =

= 2 27 ∙ ∫ - 1 2 3 y ∙ x y 2 y + 2 d y =

Calculando os limites de integração:

= 2 27 ∙ ∫ - 1 2 3 y y + 2 - 3 y ∙ y 2 d y =

Podemos colocar 3 em evidência pra fora da integral e abrir os produtos:

= 2 27 ∙ 3 ∙ ∫ - 1 2 y 2 + y - y 3 d y =

= 2 9 ∙ ∫ - 1 2 - y 3 + y 2 + y d y =

Agora integramos em função de y :

= 2 9 ∙ - y 4 4 + y 3 3 + y 2 2 - 1 2 =

= 2 9 ∙ - 2 4 4 + 2 3 3 + 2 2 2 - - - 1 4 4 + - 1 3 3 + - 1 2 2 =

Resolvendo as contas:

= 2 9 ∙ - 4 + 8 3 + 2 + 1 4 + 1 3 - 1 2 =

= 2 9 ∙ - 2 + 9 3 + 1 4 - 1 2 =

Então:

= 2 9 ∙ - 2 + 1 4 - 1 2 =

Colocando os termos dentro dos parênteses no mesmo denominador:

= 2 9 ∙ - 8 + 1 - 2 4 =

= 2 9 ∙ 9 4 ⇒ y - = 1 2

E achamos a posição do centro de massa:

x - , y - = 8 5 , 1 2

Resposta

m = 27 2

x - , y - = 8 5 , 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície.A parte do paraboloide z = 4 - x 2 - y 2 que está acima do plano x y .
Determine, com precisão de quatro casas decimais, a área da parte da superfície z = 1 + x 2 y 2 que está acima do disco x 2 + y 2 ≤ 1 .
Determine a área da superfície.A parte do cilindro y 2 + z 2 = 9 que está acima do retângulo com vértices ( 0,0 ) , ( 4,0 ) , ( 0,2 ) e ( 4,2 ) .
Determine a área da superfície.A parte do plano 3 x + 2 y + z = 6 que está no primeiro octante.
Determine a área exata da superfície z = 1 + x + y + x 2 , - 2 ≤ x ≤ 1 , - 1 ≤ y ≤ 1