Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.11 - Ex. 30

Encontre a derivada. Simplifique quando possível.

30 . f (x) = e^x senh x

Passo 1

Para resolver essa, precisaremos utilizar a regra do produto, pois temos uma multiplicação de funções g (x) = e^x e h (x) = senh x .

Fórmulas e derivadas que serão usadas

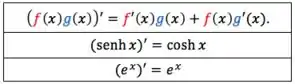
Passo 2

Aplicando a regra do produto temos:

f ' (x) = ( e^x ) ' ( senh x ) + e^x ( senh x ) '

f ' ( x ) = e^x senh x + e^x cosh x = e^x ( senh x + cosh x )

f ' (x) = e^x ( senh x + cosh x )

Agora devemos lembrar que e^x = senh x + cosh x . Ficamos então com:

f ' (x) = e^x (e^x) = e^(2 x)

f ' (x) = e^(2 x)

Resposta

f ' (x) = e^(2 x)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3 – 26 Derive.24. F (t) = (A t)/(B t^2 + C t^3)
Derivez = w^((3)/(2)) (w + c e^w)
16. Derive y = t 3 + t t 4 - 2
Derive a função: g ( t ) = t - t t 1 3
Derive a função: f ( t ) = 2 t 4 + t ² ²