Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 14

  1. Encontre os intervalos nos quais f é crescente ou decrescente.
  2. Encontre os valores máximo e mínimo local de f .
  3. Encontre os intervalos de concavidade e os pontos de inflexão.

f x = cos 2 ⁡ x - 2 sen ⁡ x , 0 ≤ x ≤ 2 π

Passo 1

Fala aí! Bora ver o que essa questão quer da gente?!

O enunciado nos da uma função f x = cos 2 ⁡ x - 2 sen ⁡ x com o intervalo 0 ≤ x ≤ 2 π

e pede algumas coisas em relação a ela:

  1. Os intervalos nos quais f é crescente ou decrescente.
  2. Os valores máximo e mínimos locais de f .
  3. Os intervalos de concavidade e os pontos de inflexão.

Pra isso a gente vai usar as derivadas primeira e segunda da função f ( x ) . Vamos nessa?!

Passo 2

Se a derivada de uma função é positiva é sinal que ela é crescente, derivada negativa a função é decrescente! Então, para responder a letra a vamos derivar f ( x ) :

f x = cos 2 ⁡ x - 2 sen ⁡ x

Para isso vamos usar a regra da cadeia:

d y d x = d y d u d u d x  

u = cos ⁡ x

Assim:

d cos 2 ⁡ x d x = d u 2 d u d cos ⁡ x d x  

d cos 2 ⁡ x d x = 2 u × s e n   x

d cos 2 ⁡ x d x = 2 cos ⁡ x s e n   x

Finalmente temos:

f ' x = 2 cos ⁡ x sen x ⁡ - - 2 cos ⁡ x

f ' x = 2 cos ⁡ x s e n   x + 1

Vamos fazer uma tabelinha com o estudo de sinal:

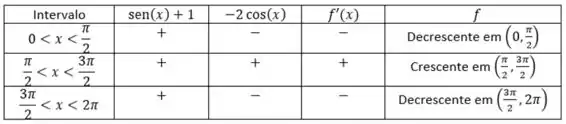
Passo 3

Agora vamos para a letra b! Para ser um ponto de máximo ou mínimo local, o sinal de f ' deve mudar nesse ponto. A tabelinha acima nos da uma boa dica!

Vemos que em x = π 2 e x = π 2 há mudança do sinal de f ' , e como em x = π 2 o sinal muda de negativo para positivo, esse é um ponto de mínimo local.

Já em x = 3 π 2 o sinal muda de positivo para negativo, então ele é um ponto de máximo local.

Para achar os valores é só substituir os valores em f :

f π 2 = cos 2 ⁡ π 2 - 2 sen ⁡ π 2 = - 2

f 3 π 2 = cos 2 ⁡ 3 π 2 - 2 sen ⁡ 3 π 2 = 2

Passo 4

Pra acabar queremos os intervalos de concavidade e os pontos de inflexão, para isso vamos calcular f ' ' ( x ) :

f ' x = 2 cos ⁡ x s e n   x + 1

Aqui vamos usar a regra do produto:

f ' ' x =

f ' ' x = - 2 - sen ⁡ x × sen ⁡ x + 1 + - 2 cos ⁡ x × cos ⁡ x

f ' ' x = 2 sen 2 ⁡ x + 2 sen ⁡ x - 2 cos 2 ⁡ x

Lembrando que:

cos 2 ⁡ x + s e n 2 x = 1

Substituindo:

f ' ' x = 2 sen 2 ⁡ x + 2 sen ⁡ x - 2 1 - sen 2 ⁡ x

f ' ' x = 4 sen 2 ⁡ x + 2 sen ⁡ x - 2

f ' ' x = 2 2 sen ⁡ x - 1 sen ⁡ x + 1

Igualamos a zero:

2 2 sen ⁡ x - 1 sen ⁡ x + 1 = 0

sen ⁡ x = - 1 2   o u   sen ⁡ x = - 1 → x = π 6   o u   x = 5 π 6   o u   x =   3 π 2

Finalmente fazemos o estudo de sinal:

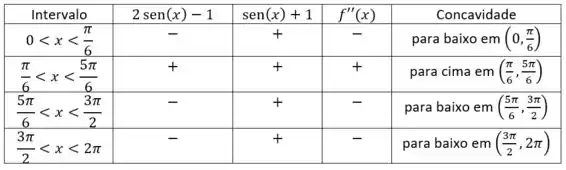
Para achar os pontos de inflexão devamos fazer f ' ' x = 0 que já fizemos em cima:

x = π 6   o u   x = 5 π 6

Para garantir que x = 3 π 4 e x = 7 π 4 são pontos de inflexão, devemos ver se f π 6 e f 5 π 6 existem:

f π 6 = cos 2 ⁡ π 6 - 2 sen ⁡ π 6 = - 1 4

f 5 π 6 = cos 2 ⁡ 5 π 6 - 2 sen ⁡ 5 π 6 = - 1 4

Temos que o ponto de inflexão são π 6 , - 1 4 e 5 π 6 , - 1 4 .

Resposta

  1. Crescente em π 2 , 3 π 2 e decrescente em 0 , π 2 e 3 π 2 , 2 π
  2. f π 2 = - 2 é mínimo local e f 3 π 2 = 2 é máximo local
  3. Concavidade para baixo em 0 , π 6 , 5 π 6 , 3 π 2 e 3 π 2 , 2 π e para cima em π 6 , 5 π 6 e ponto de inflexão são π 6 , - 1 4 e 5 π 6 , - 1 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identifique os valores extremos locais das funções nos domínios dados e informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou prog
Identifique os valores extremos locais das funções nos domínios dados e informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou prog
Identifique os valores extremos locais das funções nos domínios dados e informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou prog
Identifique os extremos locais de cada função nos intervalos dados e informe onde eles ocorremEsboce os gráficos da função e de sua derivada. Comente o comportamento de f em relação aos sinais e valor
Identifique os extremos locais de cada função nos intervalos dados e informe onde eles ocorremEsboce os gráficos da função e de sua derivada. Comente o comportamento de f em relação aos sinais e valor