Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 9
a) Encontre os intervalos nos quais é crescente ou decrescente.
b) Encontre os valores máximo e mínimos locais de .
c) Encontre os intervalos de concavidade e os pontos de inflexão.
Passo 1
Fala aí! como vai? 😁
Nesse problema foi dada a função
E nosso objetivo é determinar os intervalos em que é crescente e decrescente, obter os valores máximos e mínimos locais e tambem os locais de concavidade e pontos de inflexão.
Bastante coisa, não é? 👀
Primeiramente para determinar os intervalos de máximos e mínimos de calculamos para os valores de em que , a função é crescente, e para , a função é decresente.
Já para obter os máximos e mínimos locais, igualamos e varificamos para quais valores de a equação é satisfeita.
Agora para determinar as concavidades, calculamos e para a concavidade é para cima e a concavidade é para baixo.
E por ultimo, para obter os pontos de inflexão, fazemos
Veja só! 😉
Passo 2
Para encontrar onde é crescente ou decrescente vamos calcular a primeira derivada de :
Vamos analisar os sinais de e de :
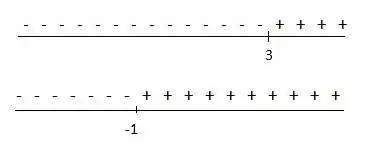
Temos que é crescente quando , e isso acontece quando:
e
E é decrescente quando , e isso acontece quando:
Tranquilo até aqui? 👀
Passo 3
Vamos obter os pontos de máximo e mínimo fazendo
Se
Nesse caso, como nossa função está fatorada, fica mais fácil, os pontos são
Para , temos
Para ...
Portanto, como o ponto é ponto de máximo e é ponto de mínimo.
Bacana, não é? 😉
Passo 4
Vamos achar para encontrar os intervalos de concavidade e os pontos de inflexão:
Para achar onde o gráfico de é côncavo para cima temos que achar o intervalo onde :
Então é côncava para cima em:
E para achar onde o gráfico de é côncavo para baixo temos que achar o intervalo onde :
Então é côncava para baixo em:
Um ponto de inflexão acontece quando a concavidade da função troca de côncava para cima para côncava para baixo, e vice-versa, achamos esse ponto em :
Vamos calcular para achar o ponto:
Pronto, temos que o ponto de inflexão é .
E aí! entendeu tudo? Responde Aí! 😬
Resposta
a) Crescente em e , decrescente em
b) é máximo local, é mínimo local
c) Côncava para cima em , côncava para baixo em , ponto de inflexão é