Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 33
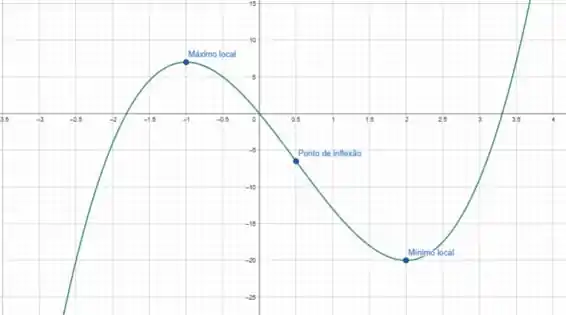
(a) Encontre os intervalos em que a função é crescente ou decrescente.
(b) Encontre os valores máximos ou mínimos locais.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use as informações das partes (a)-(c) para esboçar o gráfico. Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.
Passo 1
Oi lindos, bora resolver mais uma?
A questão pede para analisar a função em vários aspectos:
Assíntotas verticais: Elas acontecem quando tende a infinito, pra isso a gente tem que pensar em valores de que são problemáticos na função, como denominador igual a zero, raiz quadrada de um número negativo, essas coisas.
Assíntotas horizontais: Analisar o comportamento da função quando tende a .
Intervalos de crescimento e decrescimento: Encontrar os pontos críticos através da derivada primeira e analisar o sinal da derivada para determinar os intervalos.
Máximos e mínimos locais: Usar os pontos críticos e a derivada segunda ou o teste da primeira derivada para determinar a natureza dos pontos críticos.
Concavidade e pontos de inflexão: Calcular a derivada segunda e analisar seu sinal para identificar intervalos de concavidade e pontos de inflexão.
Passo 2
(a) Intervalos de Crescimento e Decrescimento
Para encontrar os intervalos onde a função é crescente ou decrescente, precisamos encontrar os intervalos onde a primeira derivada é positiva (crescente) ou negativa (decrescente).
Encontre a primeira derivada:
Os pontos críticos são encontrandos em :
Temos então que:
E
O domínio aqui da nossa função são os reais, então vamos testar aqui o valor da derivada primeira:
: temos que então esta crescendo.
: temos que então está decrescendo.
temos então que e novamente nossa função está crescendo.
Passo 3
(b) Valores Máximos e Mínimos Locais
Para encontrar os valores máximos e mínimos locais, precisamos identificar os pontos críticos, onde a primeira derivada é zero ou indefinida.
J�� encontramos eles, e são:
Teste da Derivada Segunda derivada.
Para determinar se são máximos ou mínimos, aplicamos o teste da derivada segunda. A gente vai testar esses valores dos pontos críticos na segunda derivada.
Sendo um ponto critico:
Se , então tem um mínimo local em . Isso ocorre porque a função é côncava para cima neste ponto.
Se , então tem um máximo local em . Isso ocorre porque a função é côncava para baixo neste ponto.
Se , o teste é inconclusivo. O ponto pode ser um ponto de inflexão ou pode ser necessário utilizar outros métodos para determinar a natureza do ponto crítico.
A segunda derivada é:
Derivando:
Para :
então é um máximo local.
Para
então é um mínimo local.
Passo 4
(c) Intervalos de Concavidade e Pontos de Inflexão
Para encontrar os intervalos de concavidade e os pontos de inflexão, precisamos determinar onde a concavidade da função muda.
Encontre os pontos de inflexão:
Os pontos de inflexão ocorrem quando a segunda derivada muda de sinal.
Para a concavidade muda, portanto, há um ponto de inflexão em
Intervalos de Concavidade:
Para determinar os intervalos de concavidade, devemos verificar onde (concave para cima) e (concave para baixo).
Como
a concavidade muda de côncava para cima para côncava para baixo em:
(d) Esboço do Gráfico
Agora, com todas essas informações:
- A função é crescente em
- A função é decrescente em
- Há um máximo local em e um mínimo local em
- Há um ponto de inflexão em
- A função é côncava para cima em e côncava para baixo em
Com essas informações, podemos esboçar o gráfico da função.
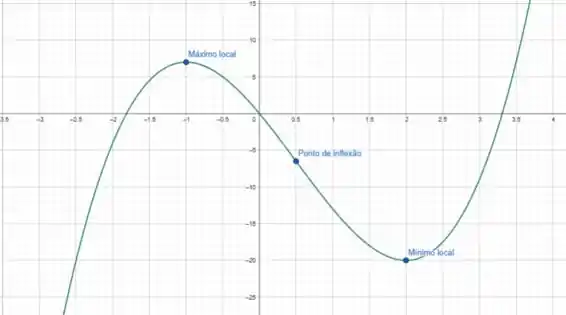
Resposta
(a) é crescente para valores de nos intervalos e e decrescente no intervalo .
(b) é ponto de máximo local e é ponto de mínimo local.
(c) possui concavidade para cima para valores de no intervalo e concavidade para baixo para valores de no intervalo . E o ponto de inflexão é .
(d)
