Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 2

Encontre a linearização L ( x ) da função em a.

2 - f (x) = s e n (x) , a = (pi)/(6)

Passo 1

Primeiramente devemos encontrar a derivada da função.

Assim:

f (x) = s e n x => f^' (x) = cos x

Passo 2

Agora precisaremos encontrar f ((pi)/(6)) e f^' ((pi)/(6))

Para isto basta substituir nas funções do passo anterior, observe:

f ((pi)/(6)) = s e n (pi)/(6) => (1)/(2)

Agora encontrando:

f^' ((pi)/(6)) = cos (pi)/(6) => (sqrt(3))/(2)

Passo 3

Agora poderemos achar L ( x ) realizando o seguinte procedimento:

f ((pi)/(6)) + f^' ((pi)/(6)) * ( x - a )

Substituindo teremos:

L (x) = (1)/(2) + (sqrt(3))/(2) (x - ((pi)/(6)))

L (x) = (1)/(2) + (sqrt(3))/(2) x - (pi sqrt(3))/(12)

L (x) = (1)/(2) (1 + sqrt(3) x - (pi sqrt(3))/(6))

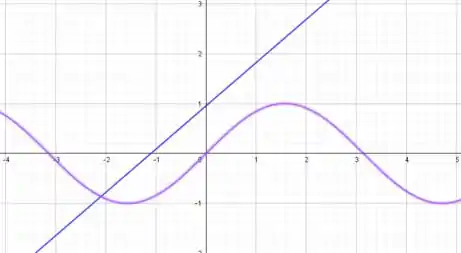
Apenas para análise segue o gráfico da função e da linearização que é a tangente em torno do ponto a = (pi)/(6) .

Resposta

L (x) = (1)/(2) (1 + sqrt(3) x - (pi sqrt(3))/(6))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-5, determine a linearização L(x) de f(x) em x = a .3- f x = x + 1 x, a = 1
Nos Exercícios 7-14, determine uma linearização em um inteiro escolhido convenientemente próximo a x 0 em que a função dada e sua derivada sejam fáceis de calcular.14- f x = s i n x - 1, x 0 = π 12
Aproximações lineares comuns em x = 0 Determine as linearizações das seguintes funções em x = 0. t gx
Nos Exercícios 7-14, determine uma linearização em um inteiro escolhido convenientemente próximo a x 0 em que a função dada e sua derivada sejam fáceis de calcular.10- f x = 1 + x, x 0 = 8.1
Aproximações lineares comuns em x = 0 Determine as linearizações das seguintes funções em x = 0 .d) e x