Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 7
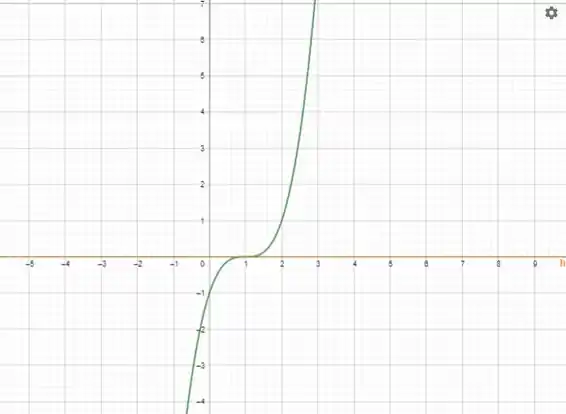
Encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da reta tangente ao gráfico nos pontos de inflexão.
Passo 1
Para analisarmos a concavidade, temos que achar a segunda derivada.
A nossa função é:
Derivando, usando a regra da cadeia para derivar o termo dentro do parênteses também:
Agora vamos para a segunda derivada, usando a regra da cadeia para derivar o termo dentro do parênteses também:
Para anaisar a concavidade, temos que olhar o sinal dessa segunda derivada.
Passo 2
Quando a segunda derivada for positiva, ela será côncava para cima.
Quando a segunda derivada for negativa, ela será côncava para baixo.
Vamos analisar quando essa derivada é positiva:
E ela vai ser negativa:
Então vamos ter:
Fazendo a classificação de concavidade:
Passo 3
Agora vamos analisar os pontos de inflexão.
Para termos ponto de inflexão, devemos ter mudança de concavidade da nossa função.
Isso acontece em , logo ele é ponto de inflexão.
Passo 4
Vamos achar a inclinação da reta tangente no ponto dfe inflexão e fazer o esboço do gráfico
Assim ela vai ter uma inclinação , vamos ver o gráfico.
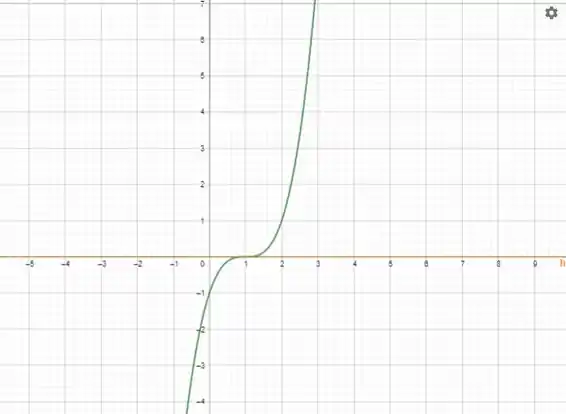
A função está em verde e a tangente em laranja
Resposta
