Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.9 - Ex. 19
19. Encontre a primitiva mais geral da função. (Verifique sua resposta derivando.)
Passo 1
E aí, suave?
A primitiva nada mais é que a integral da função, e quando integramos uma função encontramos a função que quando derivada será a do enunciado, ficou confuso? Saca a imagem que fiz para esclarecer:
Integrais e derivadas de uma mesma função são operações inversas, como a multiplicação e a divisão. Tranquilo até aqui?
Então, vamos pegar a função do enunciado, integral (encontrar a função original) e derivar, se chegarmos a mesma função do começo, acertamos a questão!
Bom galera, e para nos ajudar nessa tarefa, iremos utilizar a seguinte tabela:
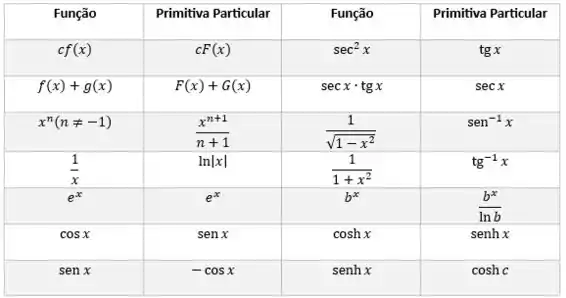
A função do enunciado é:
E sinto que estamos prontos para começar!
Passo 2
Primeiro de tudo, vamos fazer o seguinte, bora separar essa função em duas partes e encontrar as primitivas separadamente, saca só, para temos que a primitiva será:
Show de bolinhas, agora para função hiperbólica, temos , onde a primitiva é dada por:
Juntando tudo, descobrimos que a primitiva de , é dada como:
Passo 3
Irado né, agora temos a primitiva, podemos conferir o resultado derivando essa função, que fazer o processo inverso, para isso vamos usar a mesma tabela, mas agora temos a primitiva e queremos encontrar a função, logo:
Separando em partes:
Agora sim, juntando tudinho:
E assim provamos que:
E voilá, temos que a função é de fato a nossa primitiva.
