Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 44
Encontre a série de Maclaurin de (por qualquer método) e seu raio de convergência. Trace e seus primeiros polinômios de Taylor na mesma tela. O que você observa sobre a relação entre esses polinômios e ?
Passo 1
E ai meus queridooooos! Tudo na paz? Bora lá!?
Analisando a questão, percebemos que ela solicita qual a série de Maclaurin da função e seu raio de convergência. Também traçar os primeiros polinômios de Taylor e falar qual a relação entre os polinômios e a função f.
Baaah? Como faço isso?
Bom, vamos analisar a Tabela 1 e verificar se encontramos alguma série que se parece com a função .
Observe que a série para a função irá auxiliar, basta manipularmos os termos.
Já, para definir o raio de convergência aplicamos o teste da razão:
Para traçar os primeiros polinômios, após encontrarmos a série vamos expandi-la e para cada chamamos de um polinômio.
Com esse bizu, bora resolver então! Partiu!
Passo 2
Como já vimos, conhecemos a série de Maclaurin de .
Então, se substituirmos por
Como , nossa serie fica:
Passo 3
Vamos encontrar o raio de convergência dessa série.
Como já mencionado, vamos usas o teste da razão:
Logo,
Agora vamos manipular e simplificar o máximo possível:
Expandindo o fatorial do denominador duas vezes:
Logo,
O limite é , logo para todo então a série de maclaurin para o converge para todo , portanto seu raio é infinito.
Passo 4
O enunciado pede também para traçarmos o gráfico de e os primeiros polinômios da série ().
Para isso, vamos pegar a série somente até um certo grau, então os primeiros polinômios são:
E assim podemos continuar até onde quisermos.
Passo 5
Traçando e os primeiros polinômios de Taylor
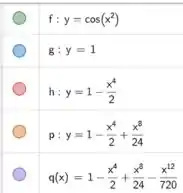
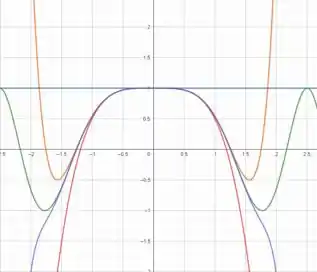
Observe que quanto maior o polinômio que pegamos (maior em ), maior a precisão em um raio maior.
Resposta
