- Se , encontre e use-o para encontrar equações das retas tangentes à curva nos pontos e .
- Ilustre a parte (a) traçando a curva e as retas tangentes na mesma tela.
Passo 1
E aí, preparado para resolver uma questão sobre derivadas e retas tangentes? Bora lá!
Aqui a gente tem a função
E iremos encontrar a equação da reta tangente a esta curva nos pontos dados. Para isso iremos precisar da derivada da nossa função nos pontos dados e a equação geral da reta tangente.
Temos que lembrar, em primeiro lugar, como achamos a derivada de . A gente faz isso com essa expressão aqui:
Essa é a definição de derivada em um ponto e a gente tem que usar ela para achar a reta tangente no ponto e no ponto .
Como estamos trabalhando com mais de um ponto, a gente vai diminuir muuuito o nosso trabalho se a gente resolver o limite de forma genérica e substituir valores só no final! Sacou?
Após realizarmos o cálculo da derivada, iremos utilizá-la na equação geral da reta tangente:
Onde é o ponto da nossa reta tangente, aqui a gente irá trabalhar com dois pontos:
Para a letra b) iremos utilizar o GeoGebra para ilustrarmos nossos gráficos, ele irá nos ajudar a termo certeza que fizermos tudo direitinho.
Dá uma olhada no que vamos fazer que vais entender direitinho!!
Passo 2
- A Nossa expressão é assim:
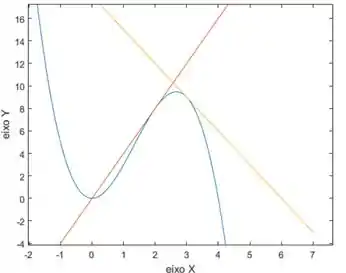
- Temos, agora, só que desenhar o gráfico da nossa curva junto com as duas retas tangentes. Olha como vai ficar:
Correto? Mas sabemos que , então a gente pode concluir que:
Beleza? A gente pega essas duas expressões e substitui no nosso limite, ficando desse jeitinho aqui:
Nós temos a nossa expressão para o limite e podemos resolvê-lo! Temos só que dar mais uma arrumada. Na nossa expressão, temos dois produtos notáveis: o quadrado da soma e o cubo da soma. Vou expandir esses produtos notáveis e vai ficar assim:
Fazendo as multiplicações necessárias e o jogo de sinal, vai ficar assim:
Podemos eliminar com e com , ficando desse jeito aqui:
Prontinho! Agora nosso limite ta arrumadão e pronto para ser resolvido!
Passo 3
Se fizermos a substituição no limite, vamos ter uma indeterminação . A gente consegue eliminar essa indeterminação colocando o em evindencia no numerador da expressão e cancelando ele com o do denominador, olha só:
Fazendo a substituição , agora teremos isso aqui:
Pronto! Encontramos uma expressão para .
Passo 4
Agora, vamos encontrar as retas tangentes nos pontos e . A reta tangente é sempre dada por:
Para o ponto , vamos ter e . Nossa expressão vai ficar assim:
A gente calcula o substituindo na expressão de , sacou? Olha só:
Pronto, temos e ele vale ! Substituindo na equação da reta tangente:
Achamos a nossa primeira reta!
Passo 5
Vamos encontrar agora a reta para o ponto . Olhando o par ordenado, a gente conclui que e . Nossa reta tangente vai ser essa aqui:
Agora, temos que encontrar . Fazemos o mesmo que no passo anterior e usamos a expressão de derivada no ponto que encontramos, dá uma olhadinha:
Substituindo na equação da reta tangente:
Uhul! Encontramos a nossa segunda reta tangente!
Passo 6
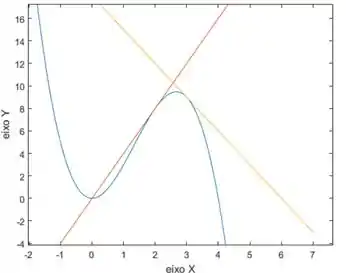
Em azul é a curva , um polinômio de grau. vermelho, temos a reta, tangente no ponto . Por último, em amarelo, teremos a reta , a qual será tangente no ponto .
Finalizamos nossa questão aqui! Ela é trabalhosa mesmo, mas esse conceito de reta tangente é muuuuito importante em cálculo e em várias outras disciplinas das ciências exatas, então faz com calma, carinho e atenção para arrasar lá na frente! ;)
Resposta
- O gráfico expressando a curva e as retas tangentes pedidas é o que segue:
Para o ponto , a reta tangente é
Para o ponto , a reta tangente é