Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 23
Encontre os vértices e os focos e as assíntotas da hipérbole e esboce o seu gráfico.
23.
Passo 1
Nessa questão, nos foi dada a equação de uma hipérbole, para encontrarmos seus vértices, focos e assíntotas.
A equação geral de uma hipérbole é , mas veja que na equação dada nós não temos nenhum número embaixo do e do , nem do lado direito. Para deixar ela mais parecida com a equação da hipérbole que estamos acostumados vamos agrupar os termos com e os termos com , completar quadrado e jogar os termos independentes para o outro lado. Muita coisa? Calma, vamos fazer passo a passo juntos:
Aqui precisamos completar quadrado, pois é assim que os termos aparecem na equação geral
Agora estamos quase lá, para fazer aparecer aquele do lado direito basta dividir a equação inteira por :
Show! Agora podemos usar essa equação para encontrar o que foi pedido.
O foco de uma hipérbole desse tipo é dado por
Como nossa equação, temos que
Passo 2
Os vértices de uma hipérbole com centro fora da origem são:
Então,
e
Passo 3
As assíntotas da hipérbole podem ser encontradas por . Neste caso temos .
Viu? Apesar do nome “assíntota da hipérbole” parecer assustador, no fim é uma coisa bem simples, nada de sofrer sem precisar.
Passo 4
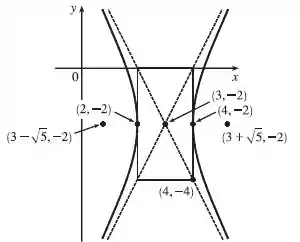
Juntando todas essas informações, podemos fazer o esboço da hipérbole:
Resposta
e