Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 7
Equações Integrais
Nos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial .
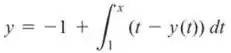
Passo 1
Como o que se deseja é uma equação diferencial, deve-se fazer a derivada da equação dada, tal que a função resultante será a que está dentro da integral, já que a derivada “anula” a integral.
Ainda, para determinar a condição inicial, será atribuído o valor no qual a integral será nula, ou seja, o mesmo valor que o limite inferior da integral.
Passo 2
Logo, fazendo a derivada da equação, tem-se:
Que será a equação diferencial equivalente de primeira ordem.
Passo 3
Em seguida, para determinar a condição inicial, o valor no qual a integral é nula nesse caso é em :
Assim, independente do valor de , a condição inicial será valida e será a condição inicial.