Esboce a área representada por . A seguir, encontre de duas maneiras: (a) utilizando a Parte do Teorema Fundamental e (b) calculando a integral usando a Parte e, então, derivando.
Passo 1
Oie, bora resolver essa questão!
Temos uma função
dada como sendo uma integral definida de uma outra função, e precisamos fazer o seguinte:
- Esboçar a área que a função representa. Lembre-se que o conceito de integral está relacionado ao conceito de área, ok?
- Calcular a derivada da função de duas maneiras distintas: usando a Parte e a Parte do Teorema Fundamental do Cálculo.
🤔 Mas o que são essas Parte 1 e Parte 2?
Bem, saca só:
- Parte - Sempre que uma função é obtida integrando uma função , então a derivada da função é a função Precisamente, se
então
- Parte - Se é uma primitiva de , ou seja, se , então
- Regra do Quociente: Se e são funções deriváreis, então:
- A derivada de é:
- Uma primitiva para é
Além disso, vale a pena relembrarmos o seguinte:
sempre que
Temos tudo o que precisamos para resolver essa questão. Bora lá 💪!
Passo 2
Vamos começar esboçando a área que a função
representa. Pensa o seguinte, quando variamos o valor de , variamos o limite superior da integral
né?
Então, a função representa a área da região entre o gráfico da função e o eixo , no intervalo Ou seja, é a área da região cinza na imagem abaixo.
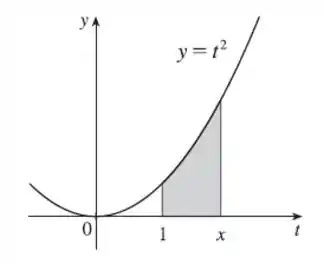
Passo 3
Item (a): Vamos usar a parte do Teorema Fundamental para calcular diretamente, sem encontrar uma expressão fechada para .
Temos que
onde
Dessa forma, como pela Parte temos que
então
Passo 4
Item (b): Agora, vamos achar encontrando primeiro e depois derivando. Para isso, vamos aplicar a Parte do Teorema Fundamental.
Temos que:
onde é uma primitiva de
Com isso, precisamos encontrar uma primitiva de Bem, pela Regra da Potência, temos que
é uma primitiva da função
Beleza! Agora que temos uma primitiva da função , vamos encontrar quem é
Observe que
ou seja,
Pronto, agora que temos uma expressão para a função , vamos derivá-la! Como
então usando a Regra da Potência e do Quociente vamos ter:
Observe que encontramos a mesma função que no Passo anterior 🎉!
Resposta
A área representada por
é a área da região cinza na imagem abaixo.
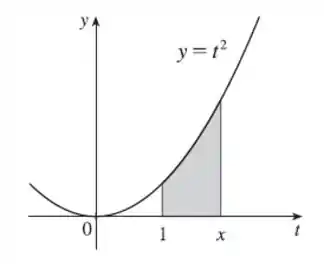
A derivada é dada por: