Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 42
Esboce a curva com equação dada.
Passo 1
O problema pede para esboçarmos a curva em coordenadas polares. Neste caso, vamos isolar primeiro:
Como o seno está dentro de uma raiz, devemos ter
Portanto, não pode assumir qualquer valor:
Para , temos que para , . Daí, conforme cresce, vai aumentando até que para (), , que é seu máximo. Em seguida, vai diminuindo até retornar para quando :
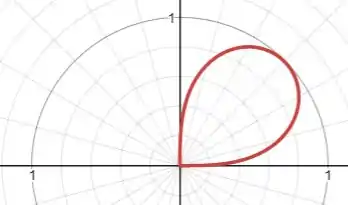
Passo 2
Para , o comportamento é o mesmo, mas como , rebatemos para o quadrante oposto:
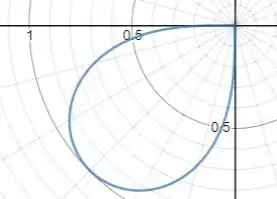
Juntando todos os pedaços, encontramos o esboço da curva:
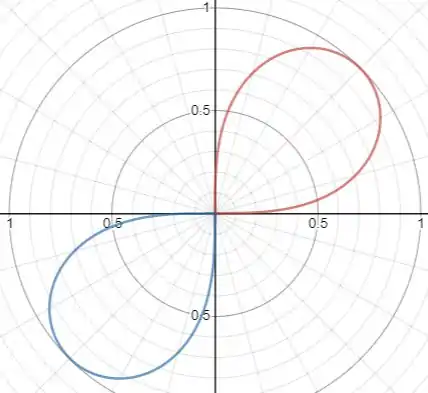
Resposta
Esboço.
Exercícios de Livros Relacionados
Encontre a inclinação da reta tangente à curva polar dada no ponto especificado pelo valor de θ .58. r = cos θ 3 , θ = π
Encontre a inclinação da reta tangente à curva polar dada no ponto especificado pelo valor de θ .60. r = 1 + 2 cos θ , θ = π / 3
Mostre que a equação polar r = a s e n θ + b c o s θ , onde a b ≠ 0 , representa um círculo, e encontre seu centro e seu raio.
A figura mostra o gráfico de r em função de θ nas coordenadas cartesianas. Use-a para esboçar o gráfico polar correspondente
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas. r 2 = c o s 4 θ