Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 7
(a) Esboce o gráfico da curva plana com a equação vetorial dada.
(b) Encontre r’(t)
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Passo 1
Olá, meu brother. Vamos resolver mais uma atividade? Veja bem.
Deveremos esboçar essa figura, para isso iremos utilizar um software gráfico. Mas antes, iremos colocar nossa curva em coordenadas cartesianas, isso irá facilitar para a gente visualizar qual o comportamento da figura do gráfico.
Para colocarmos em coordenadas cartesianas nós deveremos correlacionar as funções e de .
Para derivarmos a função é só a gente derivar cada termo do nosso vetor.
Passo 2
-
Temos que
E
Se fizermos:
Então podemos escrever
E o nosso gráfico está abaixo:
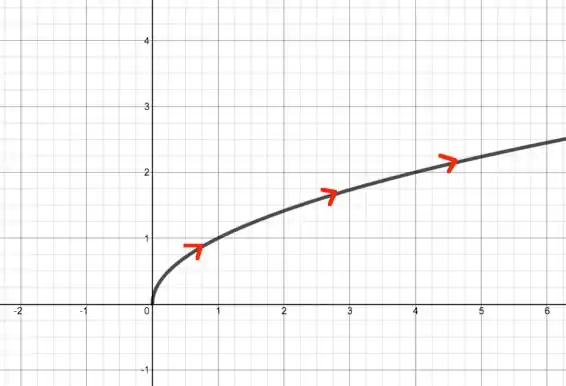
Porém veja que como não pode ser negativo, temos nosso gráfico com apenas a parte de cima.
Passo 3
-
A derivada do vetor r é dada pela derivada de cada componente:
Quando , teremos o nosso vetor tangente:
E para o vetor :
Dessa forma podemos representar os vetores:
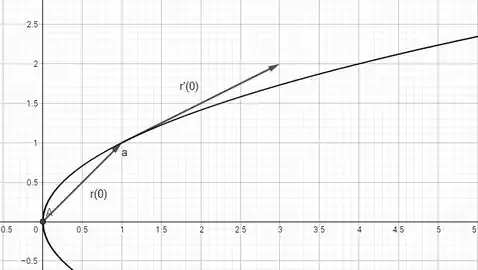
Resposta
A derivada de r é: