Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 100
Esboce o gráfico da função racional:
Passo 1
Primeiramente, vemos que o domínio da função é (não pode zerar o denominador)
Vamos calcular a derivada primeira e segunda pela regra do quociente:
Passo 2
Vamos encontrar os pontos críticos agora, que são onde a derivada é zero.
Observe que a função do numerador pode ser escrita como:
E essa função só resulta em zero se , pois não possui raiz real.
Então, nosso único ponto crítico é em , porém ele não pertence ao domínio da função, não podendo ser extremo absoluto ou relativo.
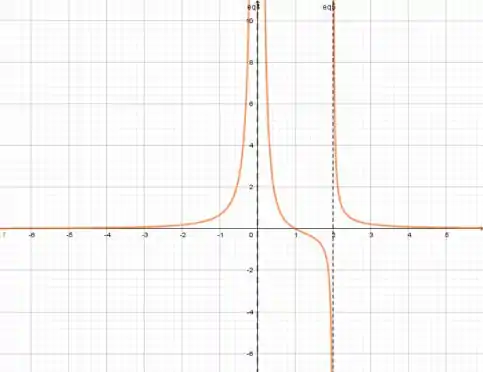
Veja que a função não está definida para e , mas está definida em todos os pontos próximos a esses. Com isso, temos assíntotas verticais em .
Passo 3
Vamos agora ver os intervalos de crescimento da função.
Vamos usar os intervalos em encontrados no passo anterior:
Então, a função é crescente em e decrescente em .
Veja que a função corta o eixo x em , então temos o ponto . E como a função deve continuar decrescente de , quando chega em a função muda a concavidade.
Então a concavidade é para cima em e e para baixo em .
Passo 4
Juntando as informações, temos o gráfico:
Resposta
Ei, a resposta está no passo a passo :)