Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.2 - Ex. 12
Esboce a solução particular e várias outras soluções. Que características estas soluções têm em comum?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A equação auxiliar da parte homogênea é:
Fatorando, temos que:
Podemos dizer que as raízes são:
Como as raízes são reais e distintas, a solução geral da EDO é da seguinte forma:
Onde e são constantes.
Passo 2
Vamos analisar a parte particular agora. Seja:
Temos que:
Derivando em relação a , temos:
Derivando novamente, temos que:
Passo 3
Agora vamos substituir na EDO.
Comparando os coeficientes de termos semelhantes dos dois lados, temos que:
Passo 4
Portanto, a solução particular é .
A solução geral é dada por:
Portanto:
Passo 5
O gráfico com a solução particular e as demais soluções vai se comportar da seguinte maneira:
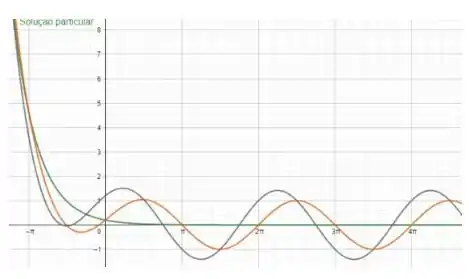
Observe que todas as soluções com excessão de oscilam ao redor de e todas as soluções se aproximam de quando .
Resposta
Ei, a resposta está no passo a passo :)