Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 3
(a) Estime a área sob o gráfico de de até usando quatro retângulos aproximantes e extremidades direitas. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou uma superestimativa?
(b) Repita a parte (a) usando extremidades esquerdas.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente estimar a área sob o gráfico de de até usando quatro retângulos aproximantes e extremidades direitas e, depois, repetir o processo usando extremidades esquerdas.
Pra a primeira aproximação, vamos esboçar o gráfico de com os quatro retângulos abaixo da curva. Assim, vamos somar as áreas dos triângulos usando a fórmula:
Repare que o intervalo é de até , com , então, temos:
Então, vamos substituir extrair alguns valores e no gráfico, substituir na fórmula e calcular nossa aproximação. Depois vamos fazer o mesmo processo na letra (b), usando retângulos nas extremidades esquerdas.
Vamos lá!
Passo 2
Vamos começar esboçando o gráfico com os retângulos da letra (a):
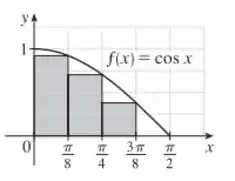
Estimando a área abaixo da curva, somando as áreas dos retângulos, temos:
Como , extraindo alguns valores de do gráfico, no intervalo considerado, vamos ter:
Então, calculando, obtemos:
Como está decrescendo em , é obtida uma subestimação usando as aproximações extremas à direita .
Passo 3
Agora vamos fazer o esboço do gráfico na letra (b):
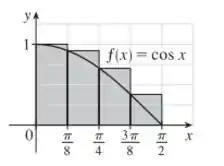
Usando a fórmula da estimativa de área:
Também com , temos:
E calculando, obtemos:
Observe que é uma superestimação.
Valeu, galera! Até a próxima! 😉