Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.5 - Ex. 4
Um estudante alega que sempre que a aproximação linear local é utilizada para aproximar a raiz quadrada de um número, a aproximação resultante é muito grande.
(a) Escreva algumas frases precisando a alegação do estudante e justifique a alegação geometricamente.
(b) Verifique a alegação do estudante algebricamente usando a aproximação (1)
Passo 1
(a)
Como a função não altera muito sua curvatura, quando aproximamos ela pra uma reta em algum ponto, essa reta fica muito próxima da curva nas redondezas do ponto, o que garante aproximações muito boas. Veja na imagem:
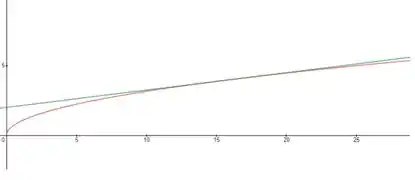
Passo 2
(b)
A aproximação (1) nos diz que:
Usando
Então:
Passo 3
Se olharmos pro erro da aproximação:
Como para valer a aproximação, temos que pegar um bem próximo de ,
E além disso, para valores maiores de a função tem uma inclinação pequena, nesses casos:
Então:
PS: perceba que esse erro é muito pequeno principalmente para valores de maiores.
Resposta
Ei, a resposta está no passo a passo :)