Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 43
Nos Exercícios de 33 a 46, esboce parte do gráfico de uma função contendo o ponto onde se as condições dadas estiverem satisfeitas. Suponha que seja contínua em algum intervalo aberto contendo
Passo 1
Para esboçar o gráfico da função, primeiro vamos fazer uma tabela com as condições dadas:
De acordo com a tabela podemos esboçar o gráfico:
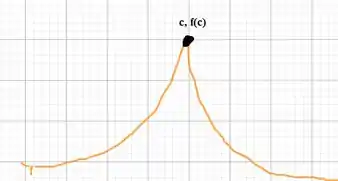
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
É dada uma tabela de sinais para as derivadas primeira e segunda de uma função. f . Supondo que f seja contínua em toda parte, encontre: (a) os intervalos em que f é crescente, (b) os intervalos em qu
É dada uma tabela de sinais para as derivadas primeira e segunda de uma função. f . Supondo que f seja contínua em toda parte, encontre: (a) os intervalos em que f é crescente, (b) os intervalos em qu
Analise as funções trigonométricas f nos intervalos especificados indicando onde f é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas x de todos os pontos de inflexão. V
Analise as funções trigonométricas f nos intervalos especificados indicando onde f é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas x de todos os pontos de inflexão. V
Analise as funções trigonométricas f nos intervalos especificados indicando onde f é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas x de todos os pontos de inflexão. V