Expresse como uma união de regiões de tipo I ou do tipo II e calcule a integral.
56.
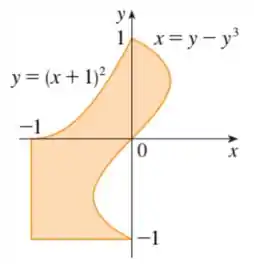
Passo 1
Fala, galera! Tudo certinho?
A questão pede para escrevermos a integral como uma região de tipo I ou tipo II, e em seguida calculá-la.
Também nos deu uma figura que mostra a área que estamos calculando, e daí achar nossos limites de integração, belê?
Passo 2
Vamos começar escolhendo nossa região.
Analisando a figura dada, percebe que no eixo temos pontos bem definidos da nossa região?
Então vamos escolher, para facilitar nossa vida, essa região como do Tipo II.
Assim, teremos que fazer a integração na ordem .
Antes disso, vamos precisar quebrar a integral em duas partes, uma com
e outra com
Para a integral acima do eixo , temos que vai da curva até .
Invertendo a primeira equação: .
Assim,
Já para a região abaixo do eixo , varia de até :
Assim, reunindo as regiões, faremos o cálculo dessa integral:
Passo 3
Fazendo a mágica acontecer, vamos começar resolvendo primeiro a integral de dentro, em relação a , em ambas as partes:
Note que podemos juntar as partes dos integrandos que são iguais em uma integral só:
Como é ímpar e e são pares, temos que:
Portanto, resolvendo em relação a , teremos
Show? 😉