Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 60
Faça um esboço da curva nos seguintes casos.
Então use esses esboços para calcular os seguintes limites
a)
b)
c)
d)
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão pede pra gente fazer o esboço da curva
Para diferentes condições de , e depois usar esse esboço para determinar os limites
a)
b)
c)
d)
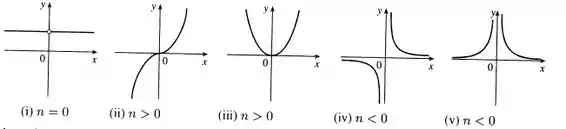
E a primeira coisa que deve chamar a nossa atenção aqui é que a nossa curva , assumirá características diferentes de acordo com os valores de que escolhermos.
Por isso é que o enunciado lista as condições:
i)
ii)
iii)
iv)
v)
Bom, então vem comigo fazer essa análise.
Passo 2
Vamos começar com
i)
então nossa função será
E qualquer coisa elevada a zero é igual a .
Então nossa função se torna:
Que é uma função constante de altura . E seu esboço será:
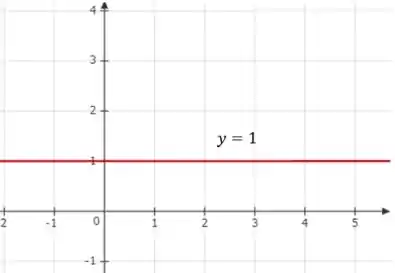
Passo 3
Agora vamos analisar a condição
ii)
Vamos supor , e , para entender o comportamento da função para esse caso.
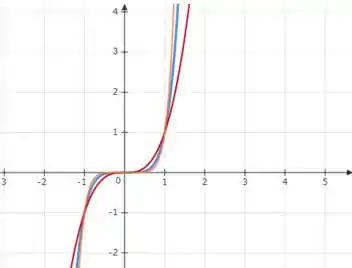
Perceba que a função tem uma característica de função ímpar, ou seja
e quanto maior for o expoente, mais rápido ele crescerá, fazendo com que a curva fique mais próxima do eixo .
Show.
Passo 4
Vamos pra próxima condição.
iii)
Vamos supor , e , para entender o comportamento da função para esse caso.
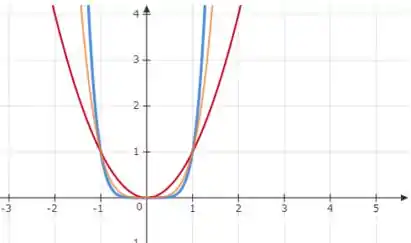
Perceba que a função tem uma característica de função par, ou seja
e quanto maior for o expoente, mais rápido ele crescerá, fazendo com que a curva fique mais próxima do eixo .
Passo 5
Vamos agora analisar
iv)
Vamos supor , e , para entender o comportamento da função para esse caso.
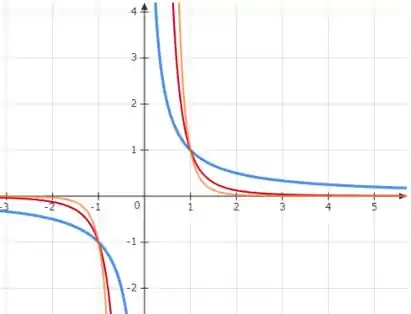
Perceba que a função tem uma característica de função ímpar, ou seja
e quanto maior for o expoente, mais rápido ela decrescerá, fazendo com que a curva fique mais afastada do eixo .
Passo 6
Vamos agora analisar
v)
Vamos supor , e , para entender o comportamento da função para esse caso.
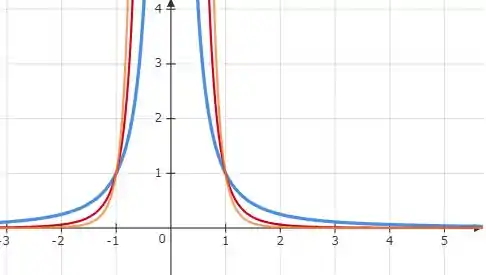
Perceba que a função tem uma característica de função par, ou seja
e quanto maior for o expoente, mais rápido ela decrescerá, fazendo com que a curva fique mais afastada do eixo .
Passo 7
Bom pessoal, agora vamos plotar as curvas pedidas em um gráfico único para entender como elas se relacionam. Podemos pegar um valor genérico que atenda os itens, apenas para visualizar o comportamento da função.
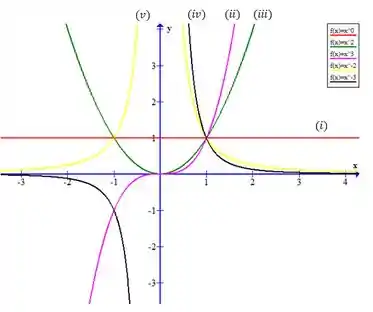
Agora, para encontrar o limite pedido, basta vermos para que valor cada uma das curvas estão se aproximando no ponto pedido. Assim, podemos ver que mostraremos todos os esboços e nos passos posteriores calcularemos os limites.
Passo 8
Pelos gráficos, podemos escrever
Pelos gráficos, podemos escrever
Pelos gráficos, podemos escrever
Pelos gráficos, podemos escrever